[1] 0.06660531[1] 0.04431304(na análise de dados phonéticos)
“I want to break p”
O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir ____________ (desconhecidos) de uma ____________ com base nos ____________ (conhecidos) de uma ____________.
O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir parâmetros (desconhecidos) de uma população com base nos dados (conhecidos) de uma amostra.
É a p____________ de se observar dados ____________ que os coletados caso a h____________ seja ____________.
É a probabilidade de se observar dados tão ou mais extremos que os coletados caso a hipótese nula seja verdadeira.
| Opção | Caras | p |
|---|---|---|
| Ca-Ca-Ca | 3 | 0.125 |
| Ca-Ca-CO | 2 | 0.125 |
| Ca-CO-Ca | 2 | 0.125 |
| Ca-CO-CO | 1 | 0.125 |
| CO-Ca-Ca | 2 | 0.125 |
| CO-Ca-CO | 1 | 0.125 |
| CO-CO-Ca | 1 | 0.125 |
| CO-CO-CO | 0 | 0.125 |
3 jogadas
6 jogadas
12 jogadas
50 jogadas
100 jogadas
sum(dbinom(90:100, 100, 0.5))1.531645e-17 \(\rightarrow 0.000000000000001531645\%\)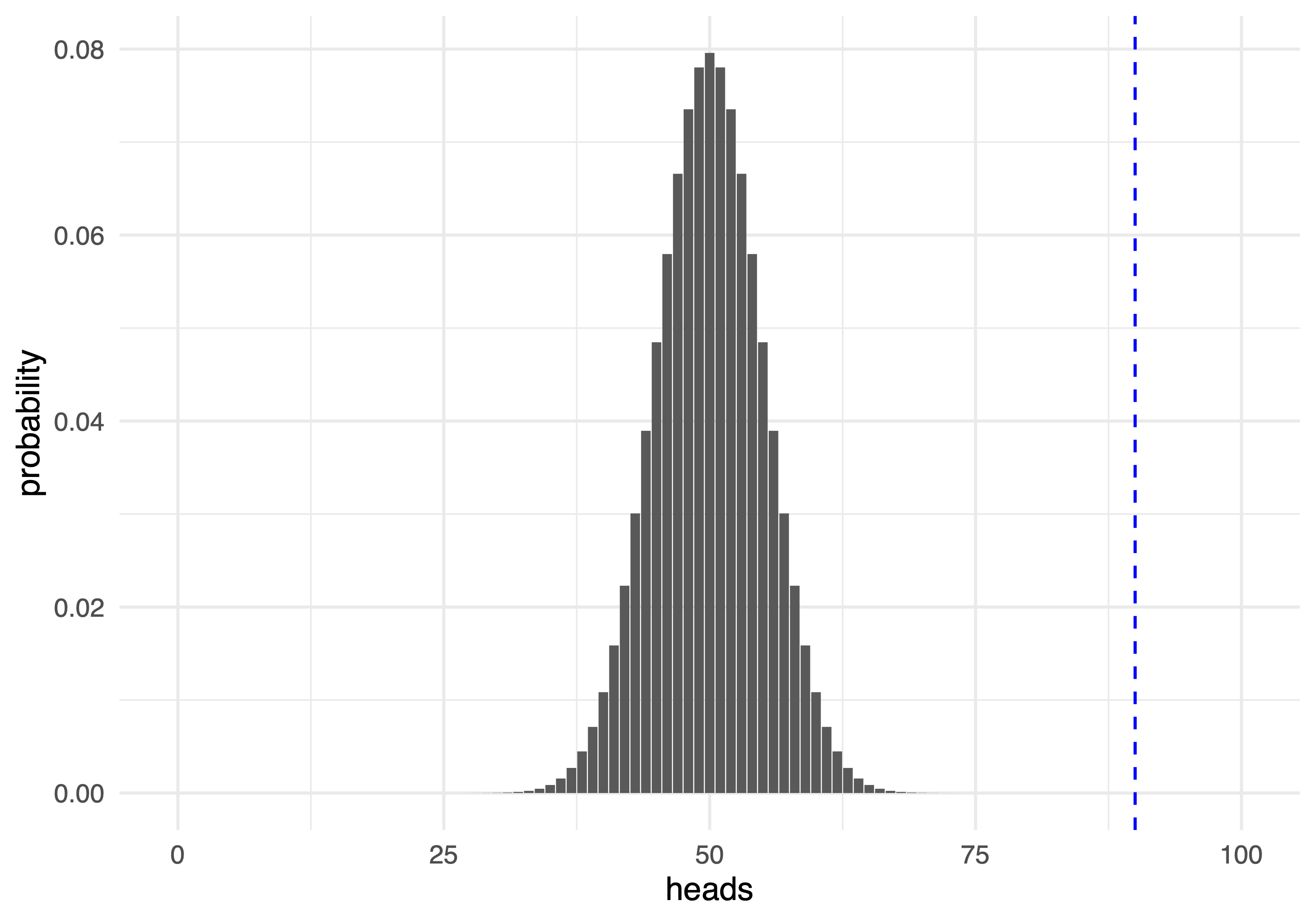
(e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015)
(e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015)
(e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015)
Por falta de conhecimento
Por decisões do pesquisador \(\rightarrow\) Vide Lima Jr. e Garcia (2021)
Por conduta antiética
(e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015)
sample1 = sample(x = population, size = 20)
sample2 = sample(x = population, size = 20)
sample3 = sample(x = population, size = 20)| class | mean | SD |
|---|---|---|
| class1 | 0.76 | 0.14 |
| class2 | 0.65 | 0.16 |
| class3 | 0.64 | 0.18 |
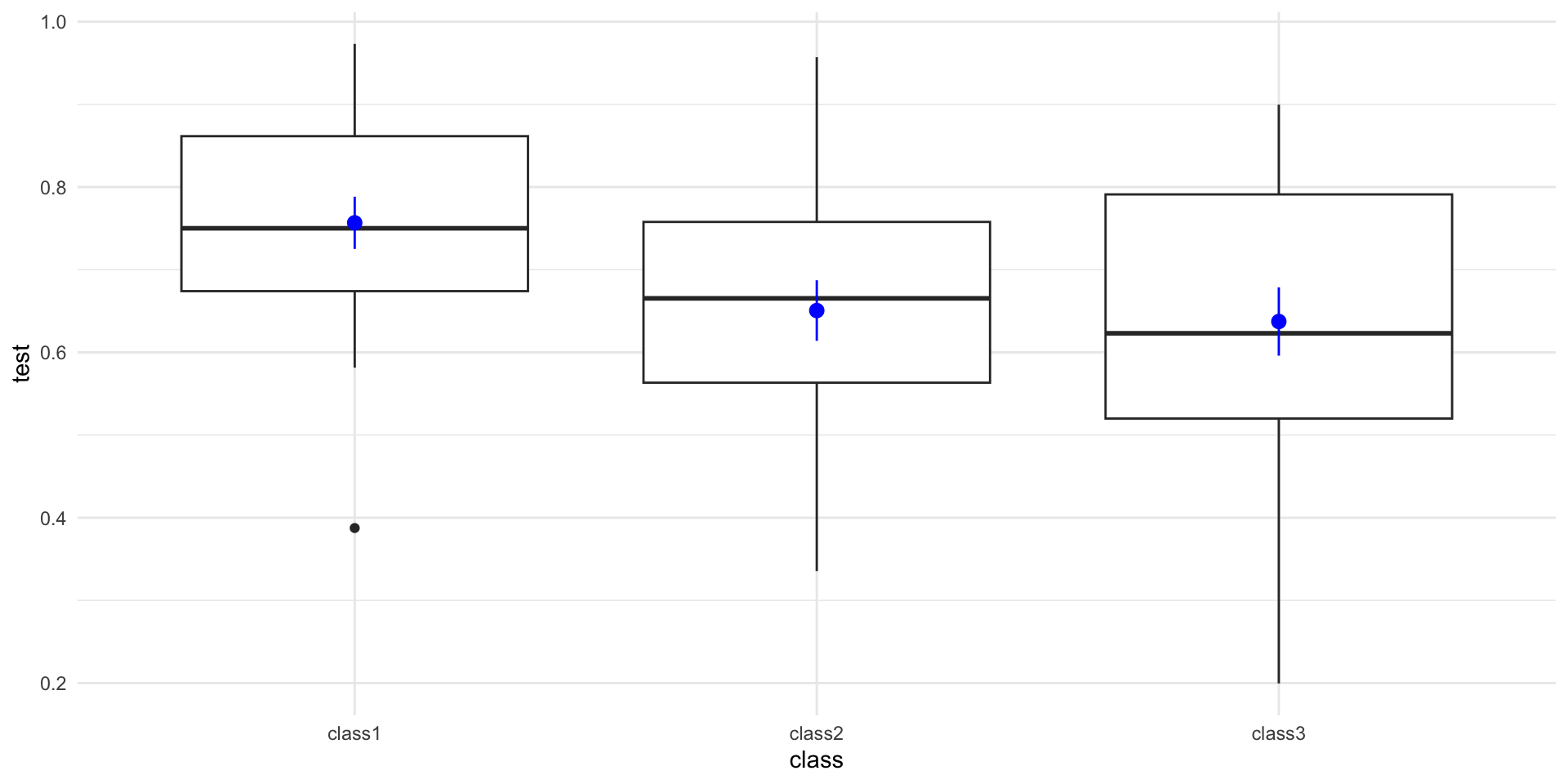
Df Sum Sq Mean Sq F value Pr(>F)
class 2 0.1713 0.08563 3.175 0.0493 *
Residuals 57 1.5374 0.02697
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Porém…
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = test ~ class, data = sample.data)
$class
diff lwr upr p adj
class2-class1 -0.10611853 -0.2310947 0.018857652 0.1111846
class3-class1 -0.11937757 -0.2443538 0.005598608 0.0640790
class3-class2 -0.01325904 -0.1382352 0.111717136 0.9647293* Valor de 0–1 que indica a probabilidade de identificar um efeito caso esteja presente
eta.sq eta.sq.part
class 0.1002268 0.1002268
Balanced one-way analysis of variance power calculation
k = 3
n = 20
f = 0.1002268
sig.level = 0.0493
power = 0.09451187
NOTE: n is number in each group
Balanced one-way analysis of variance power calculation
k = 3
n = 322.157
f = 0.1
sig.level = 0.05
power = 0.8
NOTE: n is number in each groupsample4 = sample(x = population, size = 322)
sample5 = sample(x = population, size = 322)
sample6 = sample(x = population, size = 322)| class | mean | SD |
|---|---|---|
| class4 | 0.72 | 0.15 |
| class5 | 0.70 | 0.16 |
| class6 | 0.73 | 0.15 |
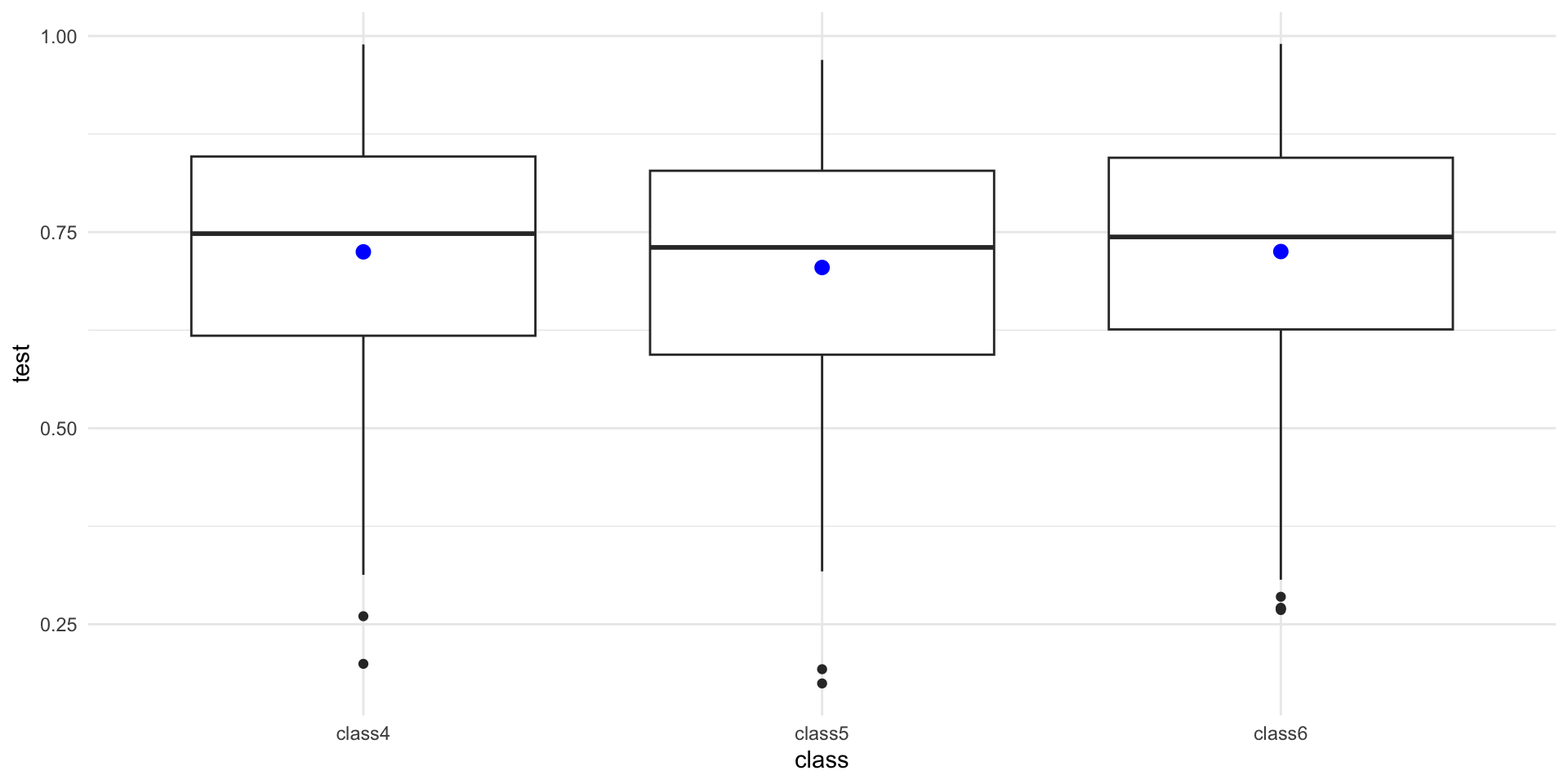
Df Sum Sq Mean Sq F value Pr(>F)
class 2 0.087 0.04351 1.83 0.161
Residuals 963 22.900 0.02378 (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015)
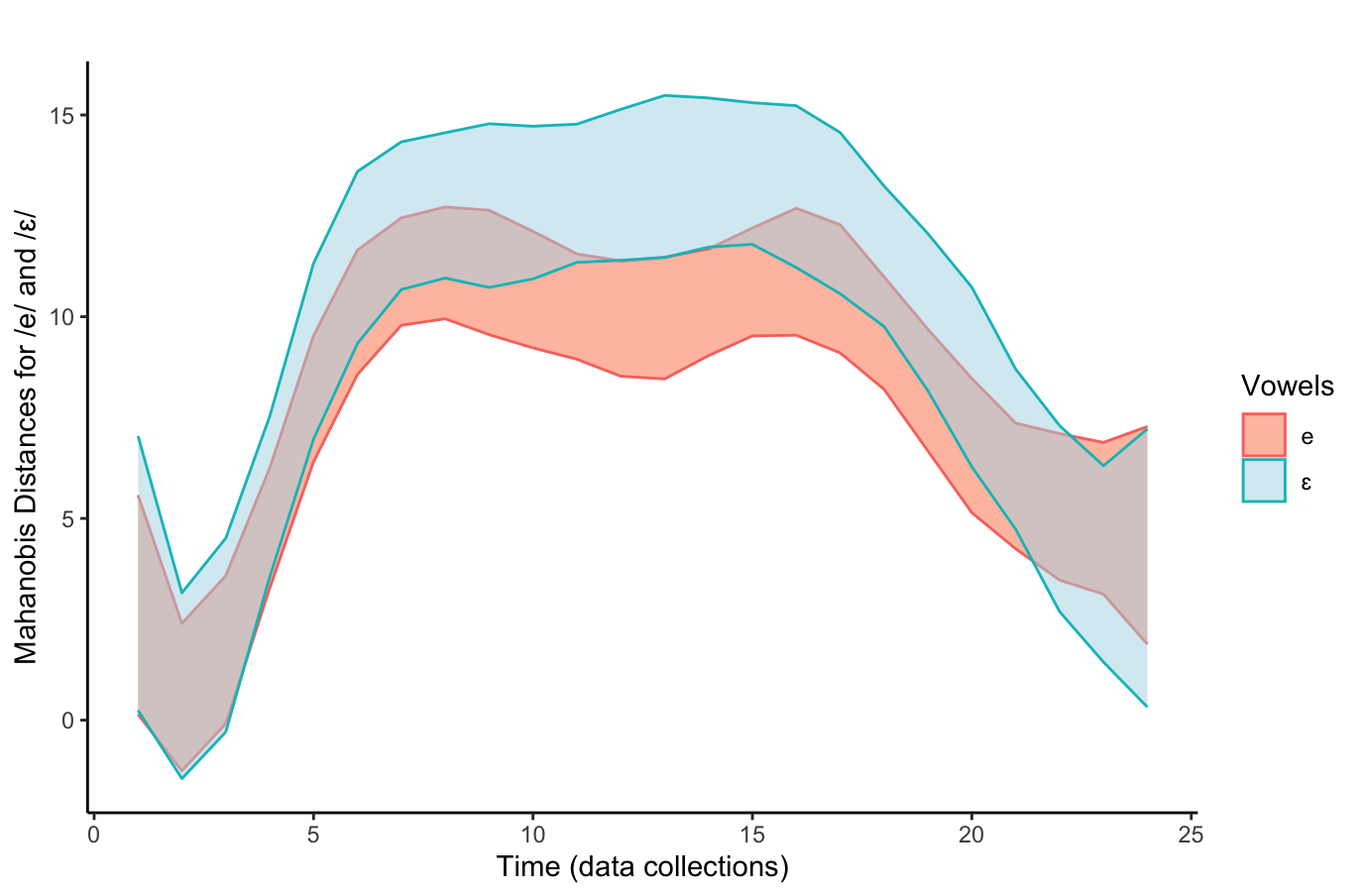
Resultado de um modelo linear que buscou verificar a influência das vogais /e ɛ/ e do tempo (24 coletas mensais) sobre a distância (de Mahalanobis) das vogais em relação à média de /e/ da primeira coleta de um aprendiz argentino de PB-L3:
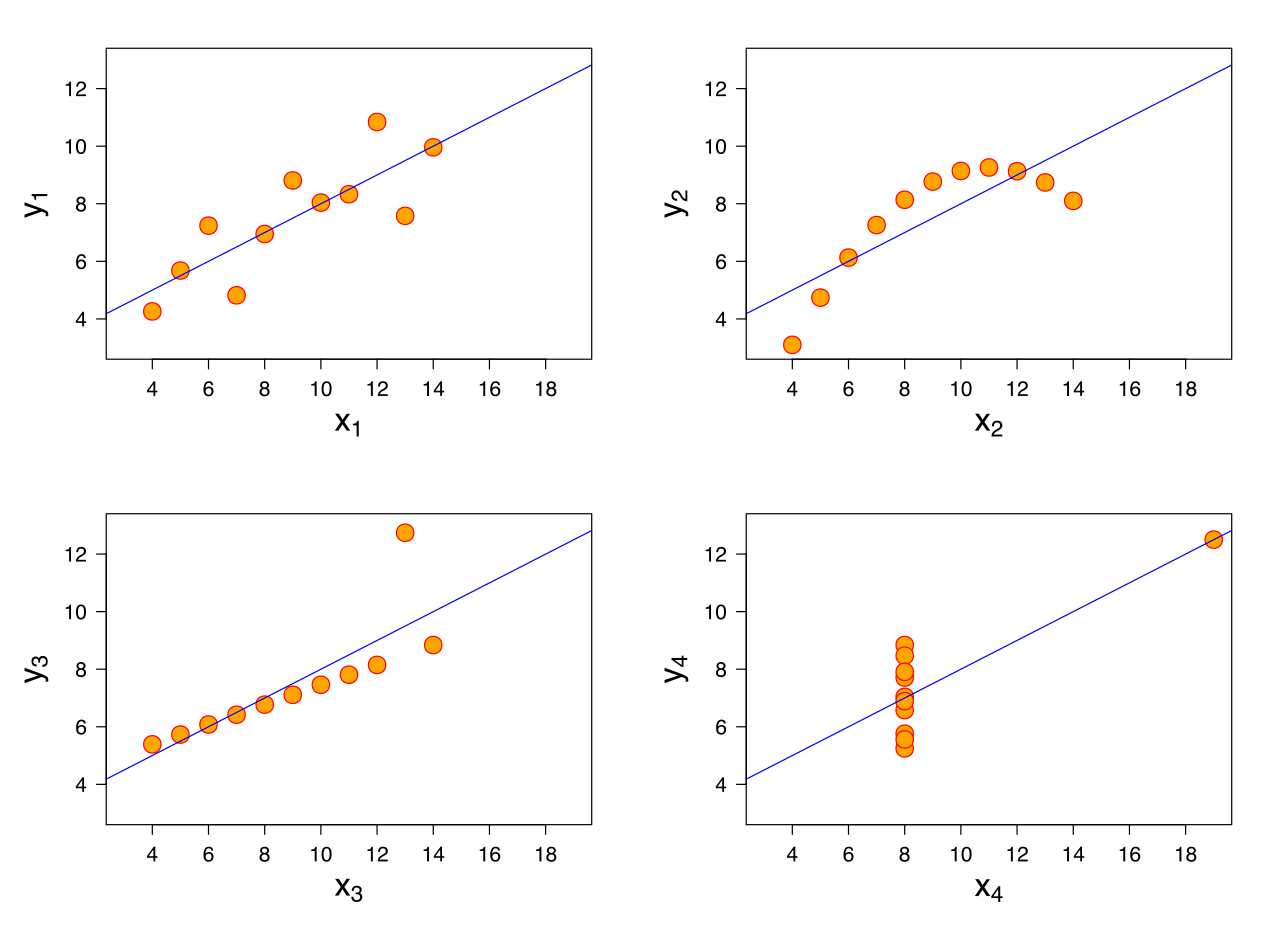
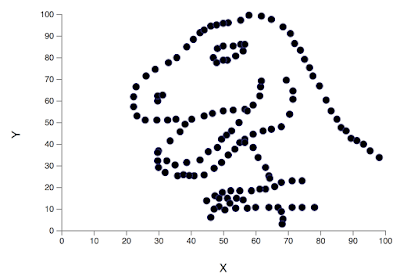
\(\bar{X}\) de x = 9
\(s\) de x = 3,3
\(\bar{X}\) de y = 7,5
\(s\) de y = 2
Corr de x e y = 0,816
Regressão linear: \(y = 3+0,5x\)
\(R^2=0,67\)

Propaganda
“Incerteza e rigor: explorando questões de dedução, intuição e probabilidade na busca científica por causalidades”
VI Encontro Intermediário do GT de Fonética e Fonologia da ANPOLL (UFPR–11 e 12 de setembro de 2024)
O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir parâmetros (desconhecidos) de uma população com base nos dados (conhecidos) de uma amostra.