## {height=5in} ["I want to break *p*"]{.fg style="--col: #e64173"} ## Objetivo da análise quantitativa O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir [____________]{.fg style="--col: #e64173"} (desconhecidos) de uma [____________]{.fg style="--col: #e64173"} com base nos [____________]{.fg style="--col: #2E86C1"} (conhecidos) de uma [____________]{.fg style="--col: #2E86C1"}. ## Objetivo da análise quantitativa O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir [parâmetros]{.fg style="--col: #e64173"} (desconhecidos) de uma [população]{.fg style="--col: #e64173"} com base nos [dados]{.fg style="--col: #2E86C1"} (conhecidos) de uma [amostra]{.fg style="--col: #2E86C1"}. . . . - Muita responsabilidade! ## {background-image="figs/meme-pvalue-PhD.png"} ## O que é o valor de *p*? . . . É a [p____________]{.fg style="--col: #e64173"} de se observar dados [____________]{.fg style="--col: #e64173"} que os coletados caso a [h____________]{.fg style="--col: #e64173"} seja [____________]{.fg style="--col: #e64173"}. ## O que é o valor de *p*? É a [probabilidade]{.fg style="--col: #e64173"} de se observar dados [tão ou mais extremos]{.fg style="--col: #e64173"} que os coletados caso a [hipótese nula]{.fg style="--col: #e64173"} seja [verdadeira]{.fg style="--col: #e64173"}. ## Exemplo {height=0.5in} - Jogo de cara ou coroa - Cara eu ganho, coroa você ganha :::{.incremental} - Qual é a probabilidade de **uma moeda justa** cair cara? - Chance de 1:2 $\rightarrow$ $1/2 = 0.5$ $\rightarrow$ $50\%$ - Qual é a probabilidade de caírem 3 caras em 3 jogadas **se a moeda for justa**? - Opções: Ca-Ca-Ca, Ca-Ca-CO, Ca-CO-Ca, Ca-CO-CO, CO-Ca-Ca, CO-Ca-CO, CO-CO-Ca, CO-CO-CO - 8 opções $\rightarrow$ $1/8 = 0.125$ $\rightarrow$ probabilidade de 12,5\% de caírem 3 caras em 3 jogadas **se a moeda for justa** ::: ## | Opção | Caras | *p* | |----------|---|-------| | Ca-Ca-Ca | 3 | 0.125 | | Ca-Ca-CO | 2 | 0.125 | | Ca-CO-Ca | 2 | 0.125 | | Ca-CO-CO | 1 | 0.125 | | CO-Ca-Ca | 2 | 0.125 | | CO-Ca-CO | 1 | 0.125 | | CO-CO-Ca | 1 | 0.125 | | CO-CO-CO | 0 | 0.125 | : {tbl-colwidths="[20,20]"} :::{.incremental} - Qual é a probabilidade de caírem 2 caras? - $0.125 \times 3 = 0.375 \rightarrow 37.5\%$ - E de caírem 2 ou mais caras? - $0.125 \times 4 = 0.5 \rightarrow 50\%$ ::: ## {width=70% fig-align="center"} ## {width=70% fig-align="center"} ## {width=70% fig-align="center"} ## {width=70% fig-align="center"} ## {width=70% fig-align="center"} ## ::: {.incremental} - Se cara eu ganho e caem 100 caras em 100 jogadas, o que você **deduz**? - Ronaldo está roubando -- a moeda é adulterada - E se caírem 99 ou 100 caras? - E se caírem 98 ou mais caras? - E se caírem 90 ou mais caras? - 50? - 51? ::: ::: {.incremental} - Qual é o seu limite? A partir de quantas caras em 100 jogadas você **deduziria** que estou roubando? [escreva este número]{.bg style="--col: #e64173"}. - $H_1$: Ronaldo está roubando -- a moeda é adulterada - $H_0$: Ronaldo não está roubando -- a moeda é justa ::: ## :::{.incremental} - Qual é a probabilidade de caírem 90 ou mais caras em 100 jogadas? - `sum(dbinom(90:100, 100, 0.5))` - `1.531645e-17` $\rightarrow 0.000000000000001531645\%$ ::: . . . {width=70% fig-align="center"} ## - Qual é a menor probabilidade que deveríamos usar para **inferir** que a $H_0$ é falsa? - Quão pequena deve ser a probabilidade de aparecerem tantas caras assim a ponto de você **inferir** que estou roubando e que a moeda é adulterada? . . . - Tradicionalmente: $5\%$ ($p < 0.05$) . . . - A partir de quantas caras em 100 jogadas a probabilidade de aparecer essa quantidade de caras ou mais é menor que $5\%$? . . . ```{r} #| echo: true sum(dbinom(58:100, 100, 0.5)) sum(dbinom(59:100, 100, 0.5)) ``` ## {width=70% fig-align="center"} . . . - O seu [número anotado]{.bg style="--col: #e64173"} de quantidade de caras a partir da qual você **deduziria** que estou roubando foi maior que 59? - Se sim, você foi mais rígido que a tradição **arbitrária** de $p<0.05$ ## O que é o valor de *p*? . . . - É a [probabilidade]{.fg style="--col: #e64173"} de se observar dados [tão ou mais extremos]{.fg style="--col: #e64173"} que os coletados caso a [hipótese nula]{.fg style="--col: #e64173"} seja [verdadeira]{.fg style="--col: #e64173"}. ## O que **NÃO** é o valor de *p*? :::{.incremental} - **não** é a probabilidade da $H_0$ ser verdadeira (é a probabilidade dos dados diante da $H_0$) - **não** prova que a $H_1$ seja verdadeira, apenas indica a decisão de rejeitar a $H_0$ (e aceitar, por responsabilidade do pesquisador, a $H_1$) - **não** indica a magnitude ou importância de um efeito -- um *p* muito baixo não indica um efeito muito alto - consequentemente, **não** existe valor de *p* "marginalmente significativo" ou "aproximando significância" - $p = 0.06$ **não** indica tendência de efeito/de diferença ::: ## 5 críticas ao valor de *p* (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015) 1. [decisão categórica que valor de *p* impõe]{.bg style="--col: #FADBD8"} ## {background-image="figs/meme-pavalue-fighter.png"} ## 5 críticas ao valor de *p* (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015) 1. decisão categórica que valor de *p* impõe 2. [arbitrariedade do 0,05 como valor limite para decisão]{.bg style="--col: #FADBD8"} ## 2. Arbitrariedade de $\alpha = 0.05$ :::{.incremental} - Basta diminuir $\alpha$? - Quanto menor o $\alpha$, menor as chances de Erro de **Tipo I**, mas maior as chances de Erro de **Tipo II** ::: ## 5 críticas ao valor de *p* (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015) 1. decisão categórica que valor de *p* impõe 2. arbitrariedade do 0,05 como valor limite para decisão 3. [possibilidade de se manipular os dados a fim de se alcançar um valor de *p* abaixo de 0,05 (*p-hacking*)]{.bg style="--col: #FADBD8"} ## 3. *p-hacking* 1. Por falta de conhecimento ## {background="#151f2b"} 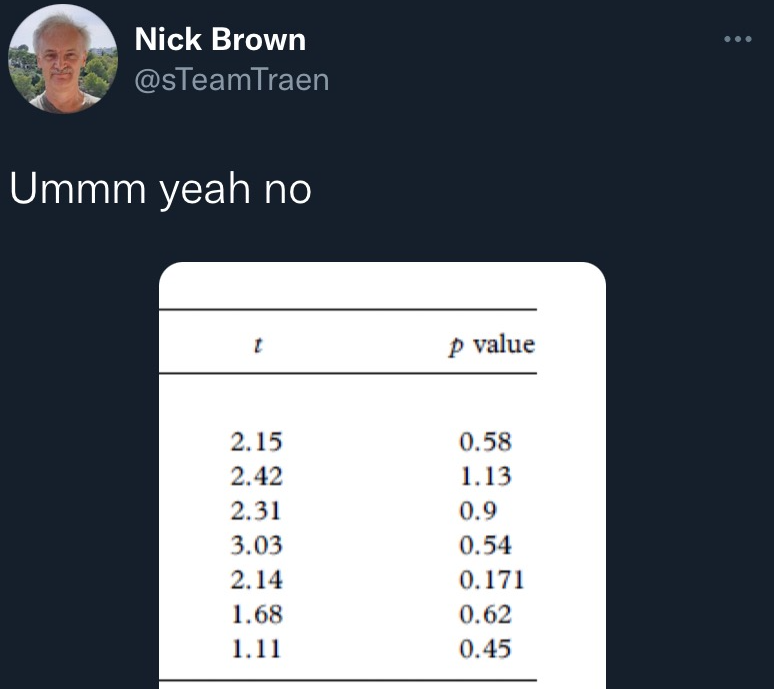{fig-align="center" width=80%} ## {background="#151f2b"} 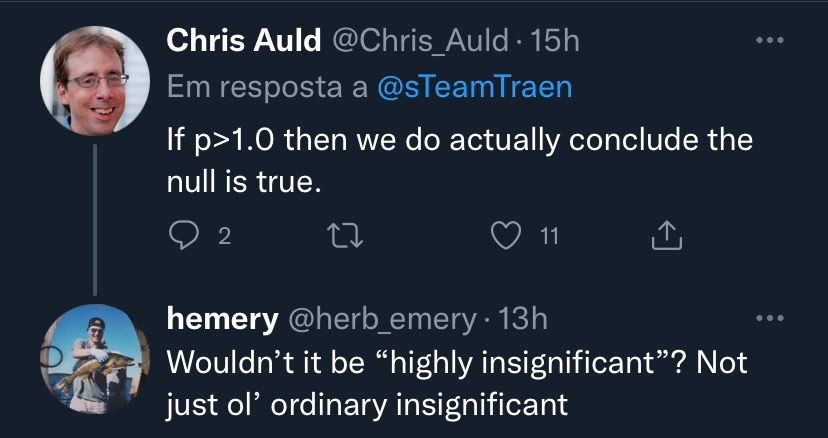{fig-align="center" width=80%} ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal - *HARKing* (*Hypothesizing After Results are Known*) ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal - *HARKing* - Comparações pareadas múltiplas ## {fig-align="center" width=80%} ## {fig-align="center" width=80%} ## {fig-align="center" width=80%} ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal - *HARKing* - Comparações pareadas múltiplas - Coletas múltiplas (mesmo indivíduo, mesmo item, etc.) ## {width=80%} ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal - *HARKing* - Comparações pareadas múltiplas - Coletas múltiplas (mesmo indivíduo, mesmo item, etc.) - Por decisões do pesquisador $\rightarrow$ Vide [Lima Jr. e Garcia (2021)](https://revista.abralin.org/index.php/abralin/article/view/1790) ## {background-iframe="https://revista.abralin.org/index.php/abralin/article/view/1790"} ## Ex.: Diferentes aproximações de *p* para modelos de efeitos mistos - *Satterthwaite’s method* ```r lmertTest::mod1 = lmer(distancia ~ gravacao + (gravacao|falante)) summary(mod1) Fixed effects: Estimate Std. Error df t value Pr(>|t|) (Intercept) 1.16050 0.12993 15.49896 8.932 1.67e-07 recording 0.14390 0.07027 9.81783 2.048 0.0683 ``` ## - *t-statistics and the normal distribution function* ```r sjPlot::tab_model(mod1) Fixed effects: Estimate Std. Error df t value Pr(>|t|) (Intercept) 1.16050 0.12993 15.49896 8.932 1.67e-07 recording 0.14390 0.07027 9.81783 2.048 0.048 ``` . . . - *conditional F-test with Kenward-Roger approximation* ```r sjPlot::tab_model(mod1) Fixed effects: Estimate Std. Error df t value Pr(>|t|) (Intercept) 1.16050 0.12993 15.49896 8.932 1.67e-07 recording 0.14390 0.07027 9.81783 2.048 0.071 ``` ## 3. *p-hacking* - Por falta de conhecimento - Teste unicaudal vs bicaudal - *HARKing* - Comparações pareadas múltiplas - Coletas múltiplas (mesmo indivíduo, mesmo item, etc.) - Por decisões do pesquisador $\rightarrow$ Vide Lima Jr. e Garcia (2021) - Por conduta antiética ## {background-iframe="https://projects.fivethirtyeight.com/p-hacking/"} ## 5 críticas ao valor de *p* (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015) 1. decisão categórica que valor de *p* impõe 2. arbitrariedade do 0,05 como valor limite para decisão 3. possibilidade de se manipular os dados a fim de se alcançar um valor de *p* abaixo de 0,05 (*p-hacking*) 4. [existência de estudos com valor de *p* abaixo de 0,05 mas com baixo poder estatístico e/ou tamanho de efeito pequeno]{.bg style="--col: #FADBD8"} ## Simular população de 100 mil alunos com seus resultados em um teste {auto-animate="true"} ``` r population = rbeta(100000, 5, 2) ``` ## Simular população de 100 mil alunos com seus resultados em um teste {auto-animate="true"} ``` r population = rbeta(100000, 5, 2) mean(population) sd(population) hist(population) ``` ## ```{r} library(tidyverse) library(DT) # Simular uma população de 100 mil alunos com seus resultados em um teste set.seed(1) population = rbeta(100000, 5, 2) hist(population) ``` ```{r} #| echo: true mean(population) sd(population) ``` ## Extrair amostras -- 3 turmas de 20 aprendizes cada ```r sample1 = sample(x = population, size = 20) sample2 = sample(x = population, size = 20) sample3 = sample(x = population, size = 20) ``` . . . ::: columns ::: {.column width="30%"} ```{r} set.seed(4) sample1 = sample(x = population, size = 20) sample2 = sample(x = population, size = 20) sample3 = sample(x = population, size = 20) # Criar um tibble (data frame) com os dados das 3 turmas simuladas (samples) sample.data = tibble(class1 = sample1, class2 = sample2, class3 = sample3) %>% gather("class1", "class2", "class3", key = class, value = test) # TAbela com médias e desvios-padrão knitr::kable(sample.data %>% group_by(class) %>% summarize(mean = mean(test), SD = sd(test)), digits = 2) ``` ::: ::: {.column width="70%"} ```{r} # Gerar gráfico ggplot(sample.data, aes(x = class, y = test)) + geom_boxplot() + stat_summary(color = "blue") + theme_minimal() ``` ::: ::: ## ANOVA ```{r} #| echo: true #| output-location: fragment summary(aov(data = sample.data, test ~ class)) ``` . . . Porém... ```{r} #| echo: true #| output-location: fragment TukeyHSD(aov(data = sample.data, test ~ class)) ``` ## Qual é o poder estatístico* dessa análise? \* Valor de 0--1 que indica a probabilidade de identificar um efeito caso esteja presente . . . - A análise do poder estatístico (de uma ANOVA) envolve 5 valores: - $k$: a quantidade de grupos - $n$: a quantidade (média) de indivíduos em cada grupo - $f$: o tamanho do efeito (no caso de ANOVAs, calculamos o $\etaˆ2$) - $\alpha$: o nível de significância (ou o valor de *p*) - **poder** . . . - Informamos 4 desses valores para que o quinto seja calculado - Antes de se conduzir um estudo para saber o $n$ ideal - Depois de conduzido para descobrir o poder ## - Para calcular o $\etaˆ2$: ```{r} #| echo: true #| output-location: fragment library(lsr) etaSquared(aov(data = sample.data, test ~ class)) ``` . . . - Sugestões de Cohen: - [$0.1$: tamanho de efeito pequeno]{.alert} - $0.25$: tamanho de efeito médio - $0.4$: tamanho de efeito grande ## - Para calcular o **poder**: ```{r} #| echo: true #| output-location: fragment library(pwr) pwr.anova.test(k = 3, n = 20, f = 0.1002268, sig.level = 0.0493) ``` . . . - Por que apenas $9,5\%$ de probabilidade de detectar um efeito caso haja um efeito? ## - Para calcular o $n$ ideal para se obter um poder de $80\%$: ```{r} #| echo: true #| output-location: fragment pwr.anova.test(k = 3, f = 0.1, sig.level = 0.05, power = 0.8) ``` ::: incremental - Seriam necessários 322 aprendizes em cada turma para se obter $80\%$ de probabilidade de detectar um efeito caso haja um - Factível? - Então o que fazer? ::: ## E se conseguíssemos 322 aprendizes em cada turma? ```r sample4 = sample(x = population, size = 322) sample5 = sample(x = population, size = 322) sample6 = sample(x = population, size = 322) ``` . . . ::: columns ::: {.column width="30%"} ```{r} set.seed(4) sample4 = sample(x = population, size = 322) sample5 = sample(x = population, size = 322) sample6 = sample(x = population, size = 322) # Criar um tibble (data frame) com os dados das 3 turmas simuladas (samples) sample.data2 = tibble(class4 = sample4, class5 = sample5, class6 = sample6) %>% gather("class4", "class5", "class6", key = class, value = test) # TAbela com médias e desvios-padrão knitr::kable(sample.data2 %>% group_by(class) %>% summarize(mean = mean(test), SD = sd(test)), digits = 2) ``` ::: ::: {.column width="70%"} ```{r} # Gerar gráfico ggplot(sample.data2, aes(x = class, y = test)) + geom_boxplot() + stat_summary(color = "blue") + theme_minimal() ``` ::: ::: ## ANOVA ```{r} #| echo: true #| output-location: fragment summary(aov(data = sample.data2, test ~ class)) ``` . . . - Agora sim, temos $80\%$ de probabilidade de detectar um efeito caso exista um, e não detectamos efeito, porque de fato sabemos que **não** há um efeito nesta população ## 5 críticas ao valor de *p* (e.g., Wagenmakers 2007, Nuzzo 2014, Halsey 2015, Kruschke 2015) 1. decisão categórica que valor de *p* impõe 2. arbitrariedade do 0,05 como valor limite para decisão 3. possibilidade de se manipular os dados a fim de se alcançar um valor de *p* abaixo de 0,05 (*p-hacking*) 4. existência de estudos com valor de *p* abaixo de 0,05 mas com baixo poder estatístico e/ou baixo tamanho de efeito 5. [o valor de *p* apresenta apenas a probabilidade dos dados diante de uma $H_0$, mas não é capaz de informar sobre a probabilidade da $H_1$ e do efeito]{.bg style="--col: #FADBD8"} ## 5. Exemplo de olhar para outras questões além do valor de *p* Resultado de um modelo linear que buscou verificar a influência das **vogais /e ɛ/** e do **tempo** (24 coletas mensais) sobre a **distância** (de Mahalanobis) das vogais em relação à média de /e/ da primeira coleta de um aprendiz argentino de PB-L3: . . . ```r lm(data = MD.e, MahalDist ~ Vowels + Coleta) Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 7.32433 0.62195 11.776 < 2e-16 *** Vowelsɛ 1.56590 0.54227 2.888 0.00398 ** Coleta 0.05736 0.03919 1.464 0.14362 ``` . . . - Pelos valores de *p*, há efeito de vogal =) - mas não de tempo =( ## Distâncias previstas pelo modelo: 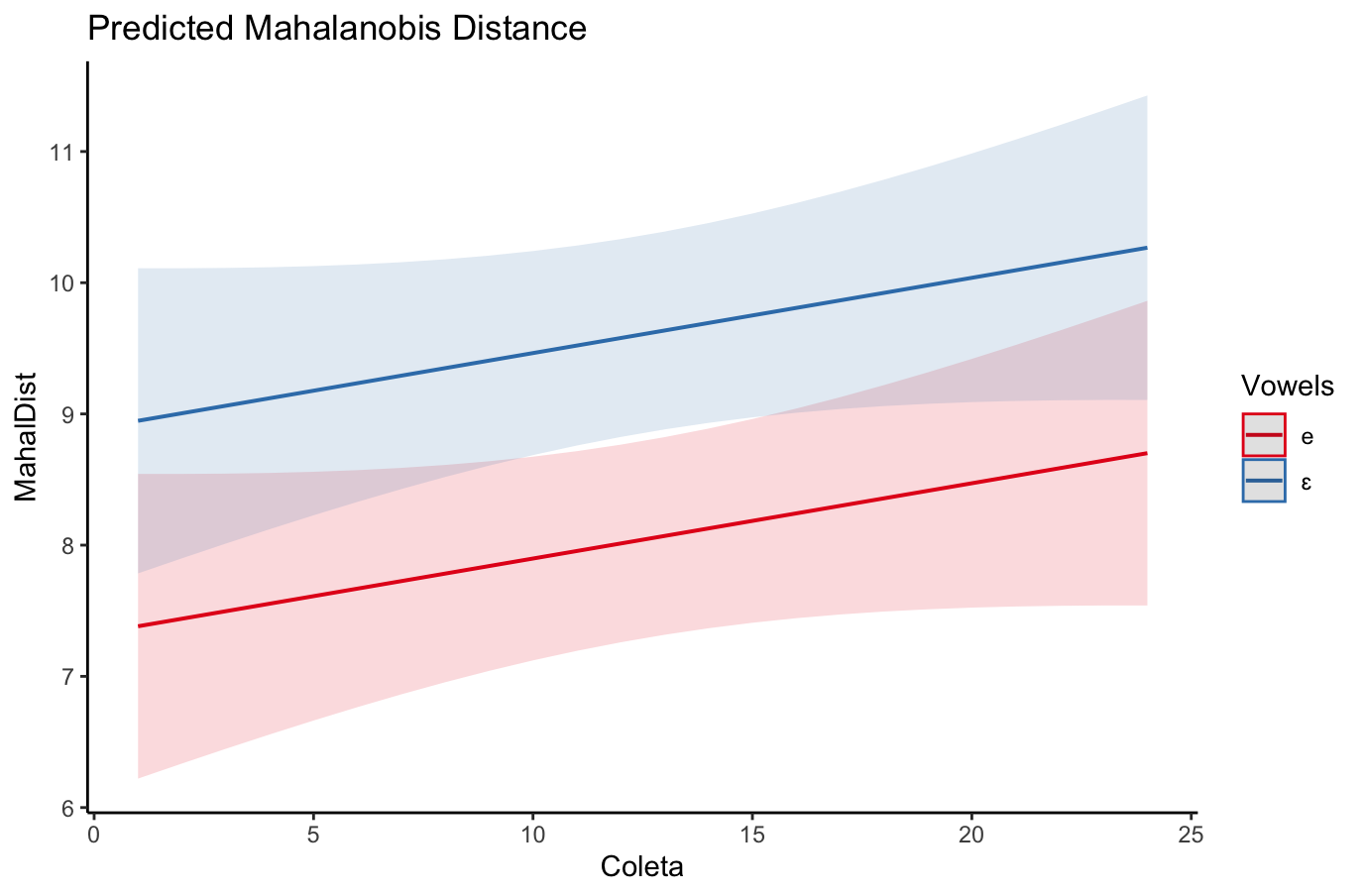{width=80% fig-align="center"} . . . - [Será?]{.fg style="--col: #C0392B"} ## Dados que geraram as distâncias e o modelo: {width=80% fig-align="center"} . . . - Será que realmente as vogais estão separadas? ## Dados das distâncias por vogal ao longo do tempo {width=80% fig-align="center"} . . . - Será que realmente não houve efeito de tempo? ## Com linhas de um modelo linear {width=80% fig-align="center"} ## Com linhas que permitem flutuação (loess) {width=80% fig-align="center"} ## Zoom nas linhas: {width=80% fig-align="center"} ## Linhas previstas por *splines* de um GAM (*Generalized Additive Model*) bayesiano: ::: columns ::: {.column width="70%"} {fig-align="center"} - Sem valores de *p* reportados ::: ::: {.column width="30%"} ::: incremental - A história fica bastante incompleta olhando-se apenas para o valores de *p* do modelo linear - A melhor escolha aqui é de um modelo que permita flutuação da linha ::: ::: ::: ## Outras lições: ::: incremental - O mundo é muito complexo, as relações são complexas, e as investigadas são desconhecidas - Há associações (correlações) espúrias ::: ## Correlações espúrias {fig-align="center"} ## {fig-align="center"} ## 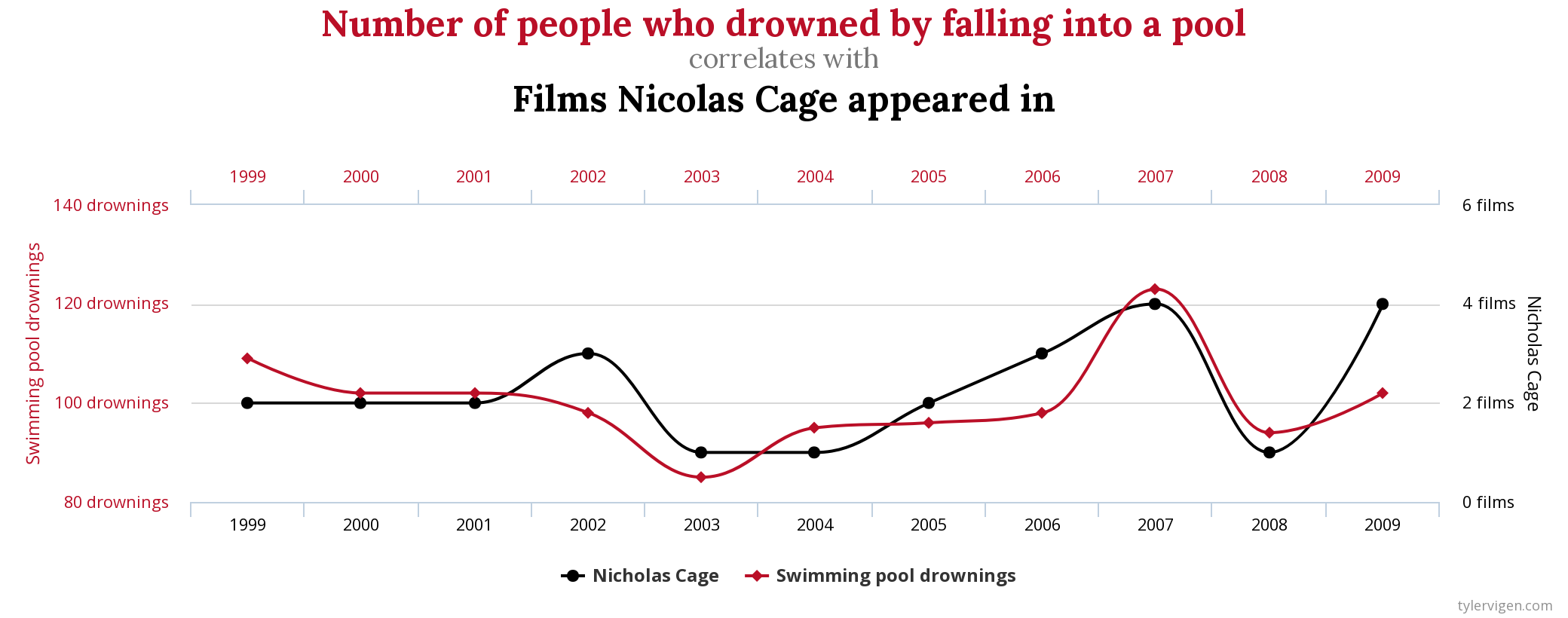{fig-align="center"} ## 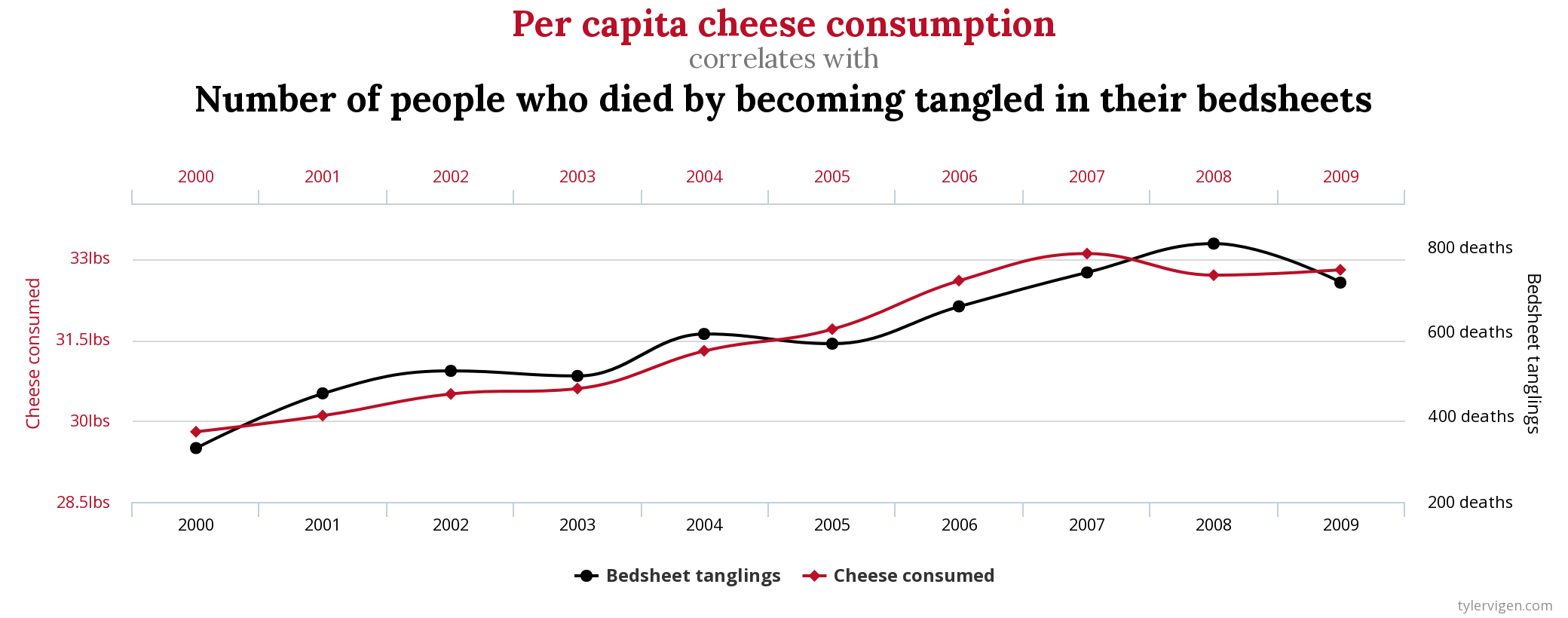{fig-align="center"} ## O quarteto de Anscombe (1973) ::: columns ::: {.column width="30%"} $\bar{X}$ de x = 9 $s$ de x = 3,3 $\bar{X}$ de y = 7,5 $s$ de y = 2 Corr de x e y = 0,816 Regressão linear: $y = 3+0,5x$ $R^2=0,67$ ::: ::: {.column width="70%"} 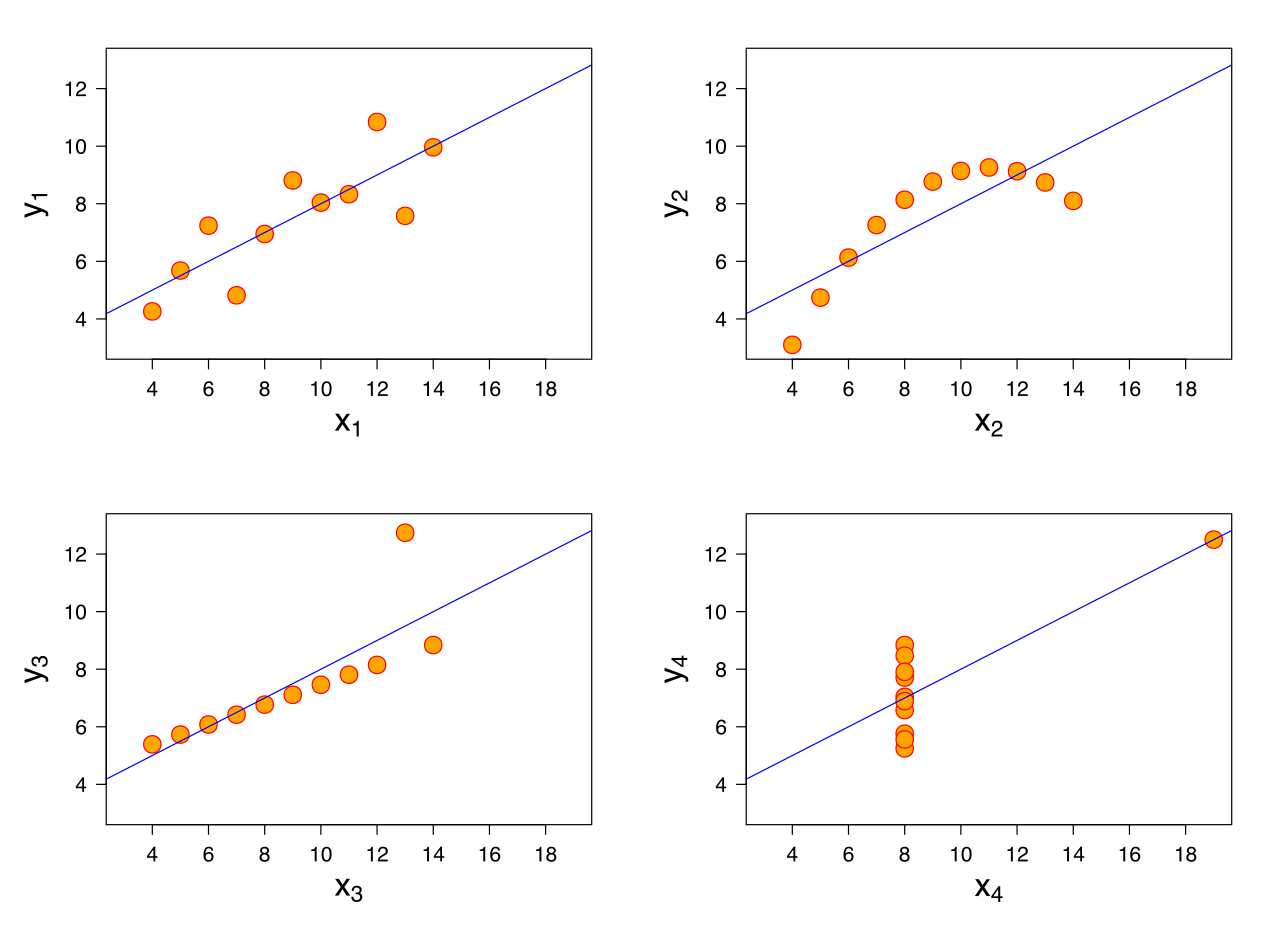{fig-align="center"} ::: ::: ## Datasaurus dozen . . . 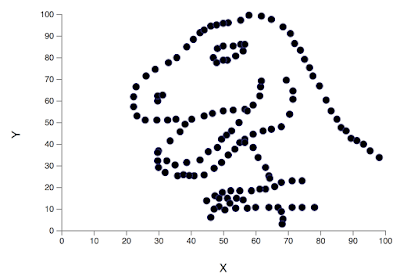{height=4in} ## Datasaurus dozen {height=6in} ## Outras lições: - O mundo é muito complexo, as relações são complexas, e as investigadas são desconhecidas - Há associações (correlações) espúrias ::: incremental - Provavelmente há diversas variáveis não investigadas envolvidas na causalidade investigada - Sempre devemos assumir que há variáveis de confusão não observadas - Nem sempre sabemos as direções das causalidades ::: ## DAGs - *Directed Acyclic Graphs* (Grafos Acíclicos Direcionados) . . . ::: {.callout-warning} ## Propaganda "*Incerteza e rigor: explorando questões de dedução, intuição e probabilidade na busca científica por causalidades*" VI Encontro Intermediário do GT de Fonética e Fonologia da ANPOLL (*UFPR--11 e 12 de setembro de 2024*) ::: ## Alternativas para o valor de *p*: - Diminuir o foco no valor de *p* e não depender apenas dele para a inferência. Investigar e reportar: - tamanho do efeito - intervalos de confiança - poder estatístico . . . - Priorizar modelos estatísticos em vez de testes de hipótese - com efeitos mistos para coletas repetidas . . . - Utilizar modelos estatísticos que nem mesmo utilizam valores de *p* e que investiguem a probabilidade da hipótese de trabalho diante dos dados (estatística bayesiana - [*stay tuned for 2025*!]{.fg style="--col: #e64173"}) ## Objetivo da análise quantitativa (retomando) O grande problema do pesquisador, e consequente objetivo da estatística inferencial, é inferir [parâmetros]{.fg style="--col: #e64173"} (desconhecidos) de uma [população]{.fg style="--col: #e64173"} com base nos [dados]{.fg style="--col: #2E86C1"} (conhecidos) de uma [amostra]{.fg style="--col: #2E86C1"}. ::: {.incremental} - Muita responsabilidade! - Reportar com cautela (modalizando) - Investigar e reportar mais informações - Acrescentar gradiência (dúvida) às inferências - Conhecer bem o que representa e quais são as limitações do valor de *p* e reportá-lo de acordo com esse conhecimento - Pensar na **significância linguística**! ::: ## {fig-align="center"} [ronaldolimajr.github.io]() [ronaldo.junior@unb.br]()