Call:
lm(formula = altura ~ idade, data = ex1)
Coefficients:
(Intercept) idade
62.504 7.545 Introdução a Análise Quantitativa de Dados para estudos fonéticos e fonológicos
Regressão Linear
Análise quantitativa de dados na Linguística
Séc. XX \(\rightarrow\) Estruturalismo e Gerativismo
- Objeto da Linguística como estrutura invariável, sistema de oposições, inato, discreto e categórico
- Levou a introspecção e dados/exemplos autocunhados
“Large groups of people make up all their utterances out of the same stock of lexical forms and grammatical constructions. A linguistic observer therefore can describe the speech-habits of a community without resorting to statistics.” (Bloomfield 1935: 37)
Séc. XX \(\rightarrow\) Estruturalismo e Gerativismo
- Objeto da Linguística como estrutura invariável, sistema de oposições, inato, discreto e categórico
- Levou a introspecção e dados/exemplos autocunhados
“I think we are forced to conclude that grammar is autonomous and independent of meaning, and that probabilistic models give no particular insight into some of the basic problems of syntactic structure.” (Chomsky 1957: 17)
Hoje
- Abordagens baseadas no uso, variação e mudança
- Dados de corpora, questionários, experimentos, correlatos físicos, construtos da psicologia, etc.
- psicolinguística, linguística de corpus, fonética/fonologia, sociolinguística, linguística aplicada, aquisição de L2, linguística forense, aprendizagem de máquinas, etc.
- e mesmo subáreas “tradicionais” que não utilizavam (sintaxe, fonologia, etc.)
- Como saber se de 3%, 5%, 8%, 10%, etc. na fala de pessoas de dois estados, de duas faixas etárias, etc. é aleatória ou efeito?
Objetivos da Análise Quantitativa de Dados
- Descrever
- Explicar
- Prever
Antes da Coleta de Dados
Problema \(\rightarrow\) Pergunta(s) \(\rightarrow\) Hipótese(s) \(\rightarrow\) Verificar/Observar/Testar \(\rightarrow\) Inferência/Conclusão
- Ex. 1: encontrar o melhor preço para um produto
- Ex. 2: motivos de lentidão em um novo percurso
Passos ANTES da coleta de dados
- identificar/caracterizar o problema
- estudar a literatura (teoria, construtos, métodos, resultados, variáveis, lacunas, etc.)
- observar o fenômeno e raciocínio dedutivo por parte do pesquisador
- compilar variáveis passíveis de influência
- estipular hipóteses
- falsiáveis e testáveis
- H1 e H0 (somadas devem abarcar todos possíveis resultados)
Passos ANTES da coleta de dados
- identificar/vislumbrar variáveis de confusão
- pensar nas direções das possíveis causalidades
- pensar em como operacionalizar as variáveis (observar, medir, contar)
- medir errado não tem conserto!
- pensar em amostras equilibradas e o mais randomizada possível
Problemas de operacionalização
Devemos desenvolver uma rotina de racioncínio questionador
- “Ação com gêmeos idênticos mostra que mascar chiclete dá uma boa impressão”
- The stuff of thought (Steven Pinker)
- “Pesquisa mostra que correr pode ser prejudicial a saúde”
- HARKing
Análise Quantitativa de Dados
O que não faremos:
- Testes de Hipótese (Null-Significance Hypothesis Testing):
- Teste de Proporção e Qui-quadrado
- Teste-t
- Teste de correlação
- ANOVA
- Testes não paramétricos
- Wilcoxon
- Kruskal-Wallis
- Friedman
- Spearman
Por quê?
O que faremos?
Modelos de Regressão
- Utilizáveis para qualquer tipo de dado/desenho experimental
- linear, logístico, ordinal, poisson, multinominal
- Exige menos requisitos (assumptions) dos dados
- O resultado já é o tamanho do efeito
- Informa por padrão o poder explicativo do modelo
- pode incorporar interações e efeitos mistos
Princípios básicos de regressão
Precisamos partir de uma correlação
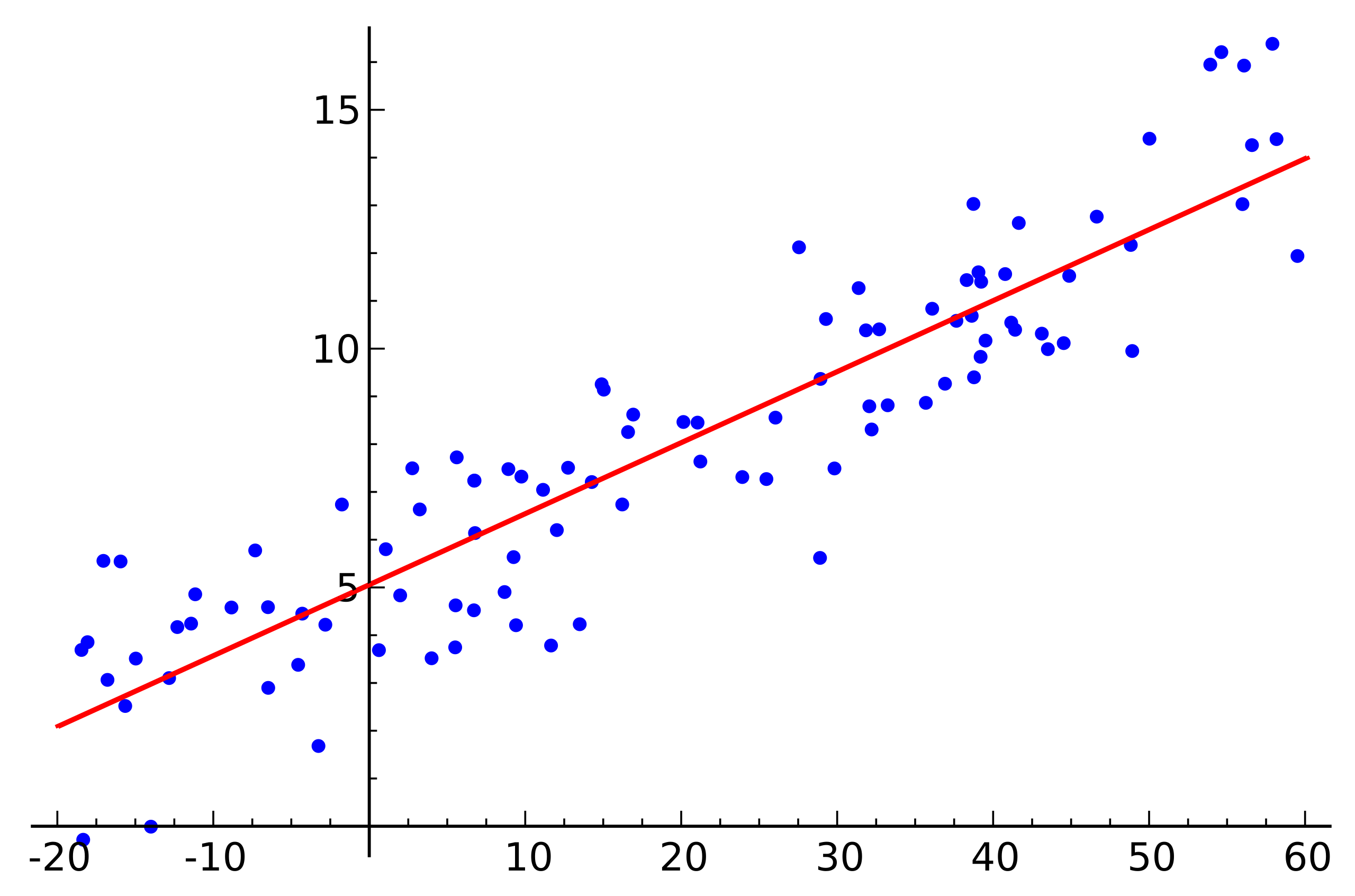
Possíveis associações entre variáveis:

- Correlação é um requisito para regressão
- Precisa haver associação entre variáveis para haver efeito
- Porém
- correlação não implica motivação
- correlation does not mean causation
Objetivos
- Verificar se há uma relação entre variáveis
- Correlação e regressão
- Prever valores não observados
- Regressão
Regressão Linear Simples
- Modelos de Regressão estimam o valor de \(y\) baseado no valor de \(x\)
- \(y =\) variável de resposta (variável dependente)
- \(x =\) variável preditora (variável independente)

Modelo de Regressão Linear Simples
- Linear: a variável de resposta deve ser numérica (contínua)
- Simples: apenas uma variável preditora
- pode ser numérica ou categórica
Modelo de Regressão Linear Simples
- Estima-se o valor de \(y\) em função do valor de \(x\)
- \(y\) ~ \(x\)
- Para desenhar a reta de regressão, utilizamos a equação linear
- \(y = a+bx\)
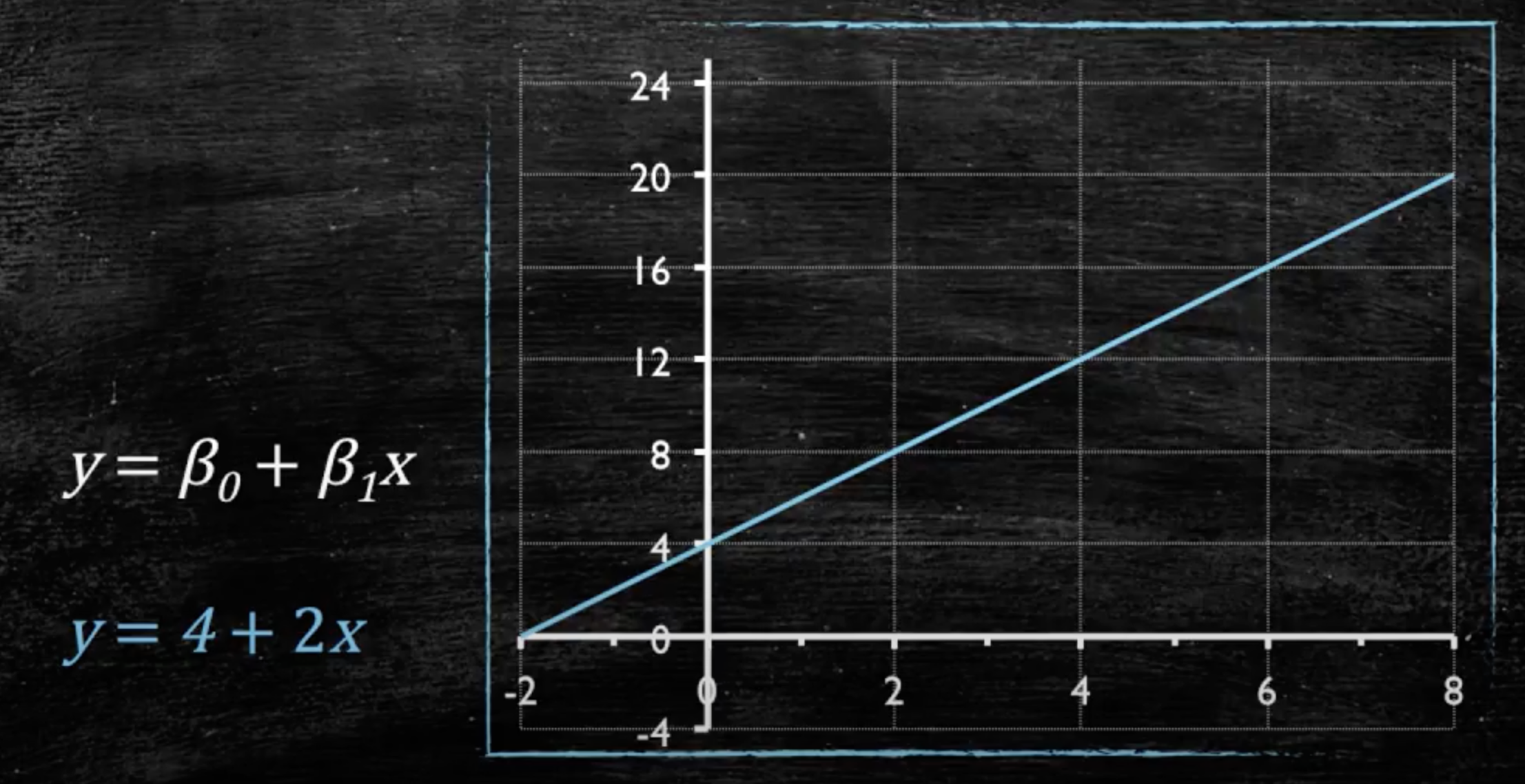
- \(y = \beta_0+\beta_1x\)
- \(y\) é o valor a ser estimado – variável de resposta
- \(x\) é o valor em função do qual a estimação será feita – variável preditora
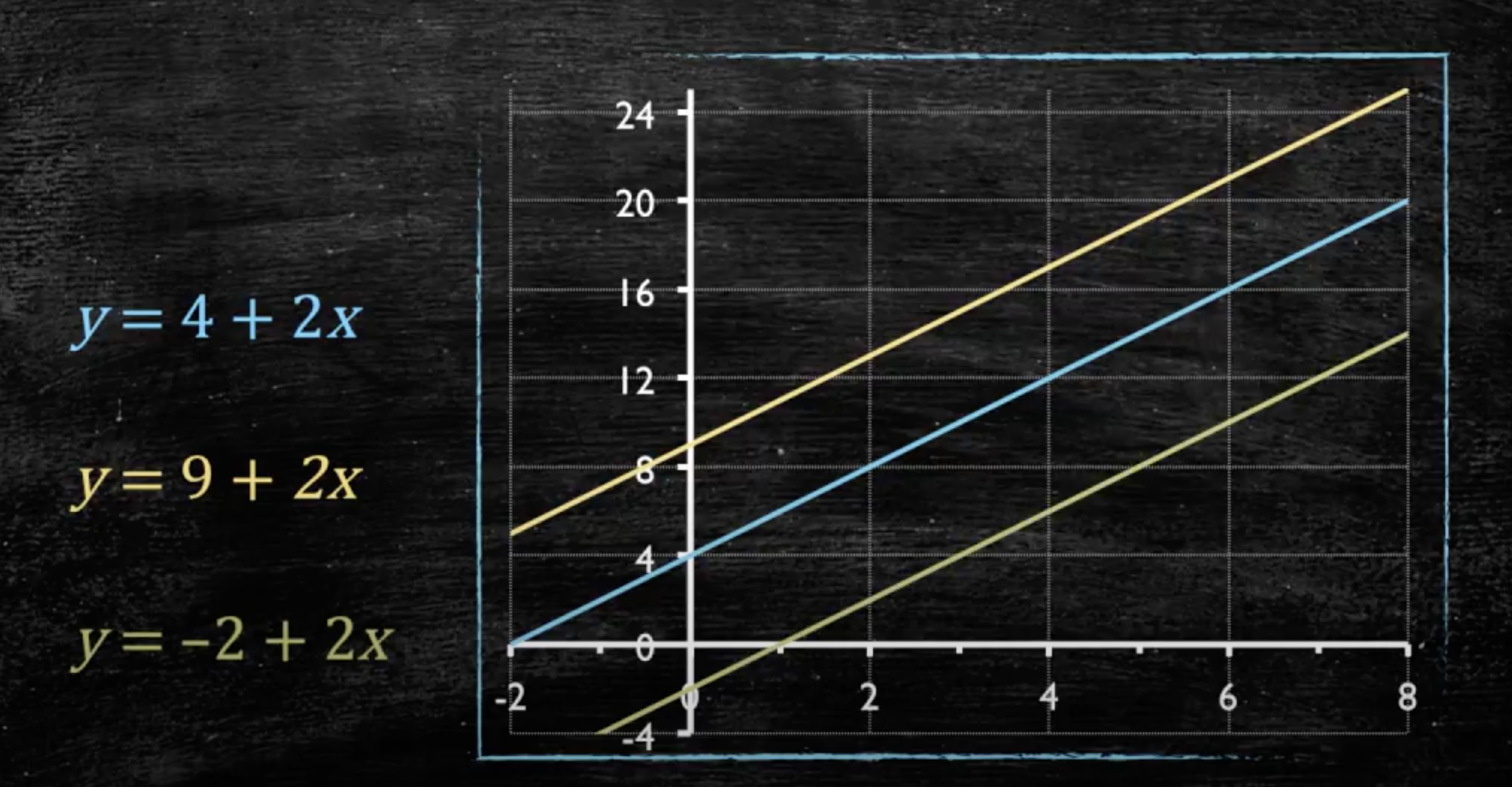
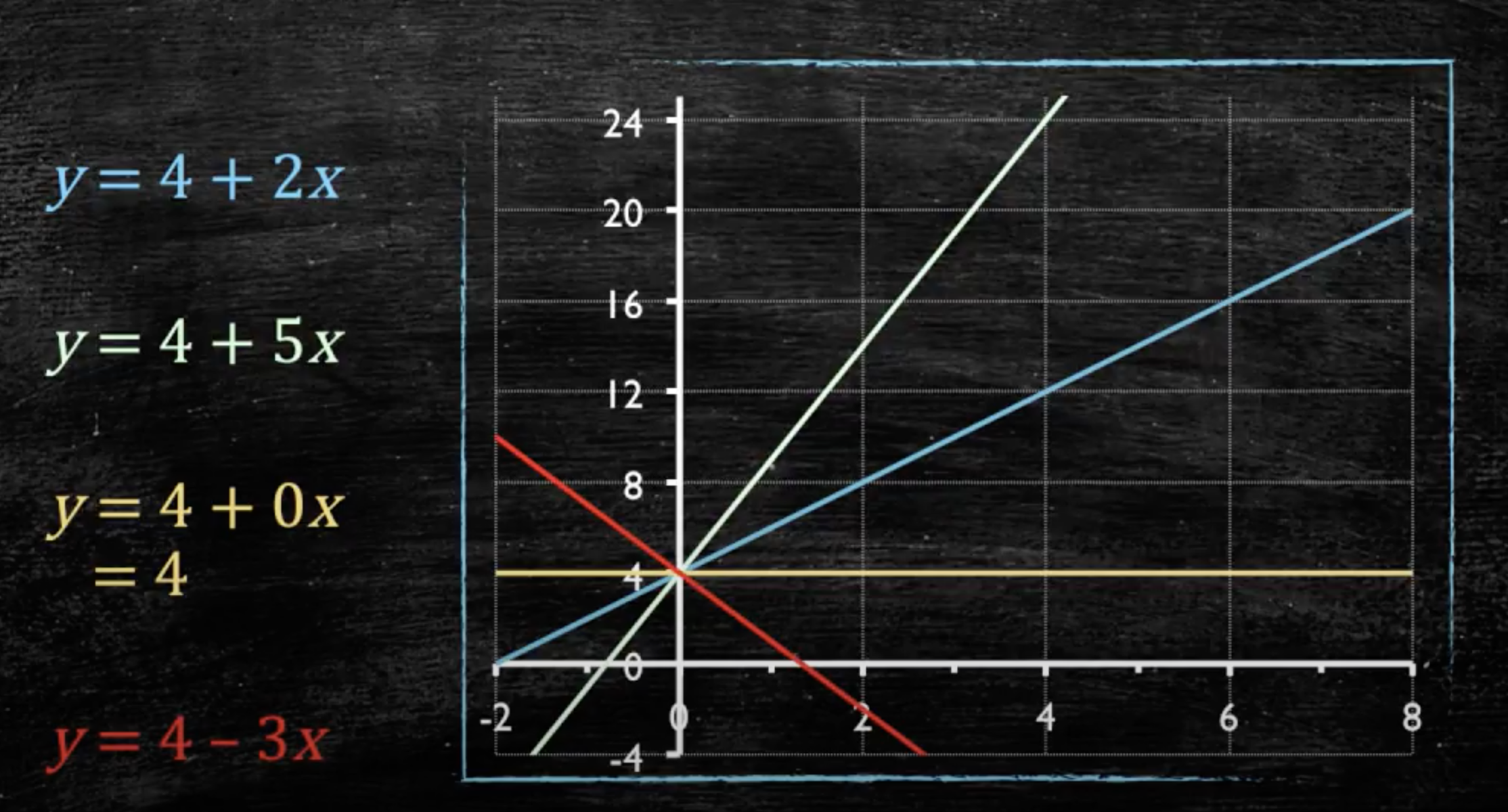
- \(\beta_0\) e \(\beta_1\) são coeficientes fornecidos pelo modelo
- \(\beta_0\) diz onde a reta começa
- \(\beta_1\) diz o ângulo da reta
- Coletamos dados \(\rightarrow\) informamos dados ao modelo (vários valores de \(x\) e de \(y\)) \(\rightarrow\) modelo calcula \(\beta_0\) e \(\beta_1\) e desenha a reta \(\rightarrow\) usamos a reta para prever valores não observados
- valor observado \(-\) valor estimado \(=\) resíduo
- o modelo desenha uma reta gerando os menores resíduos possíveis
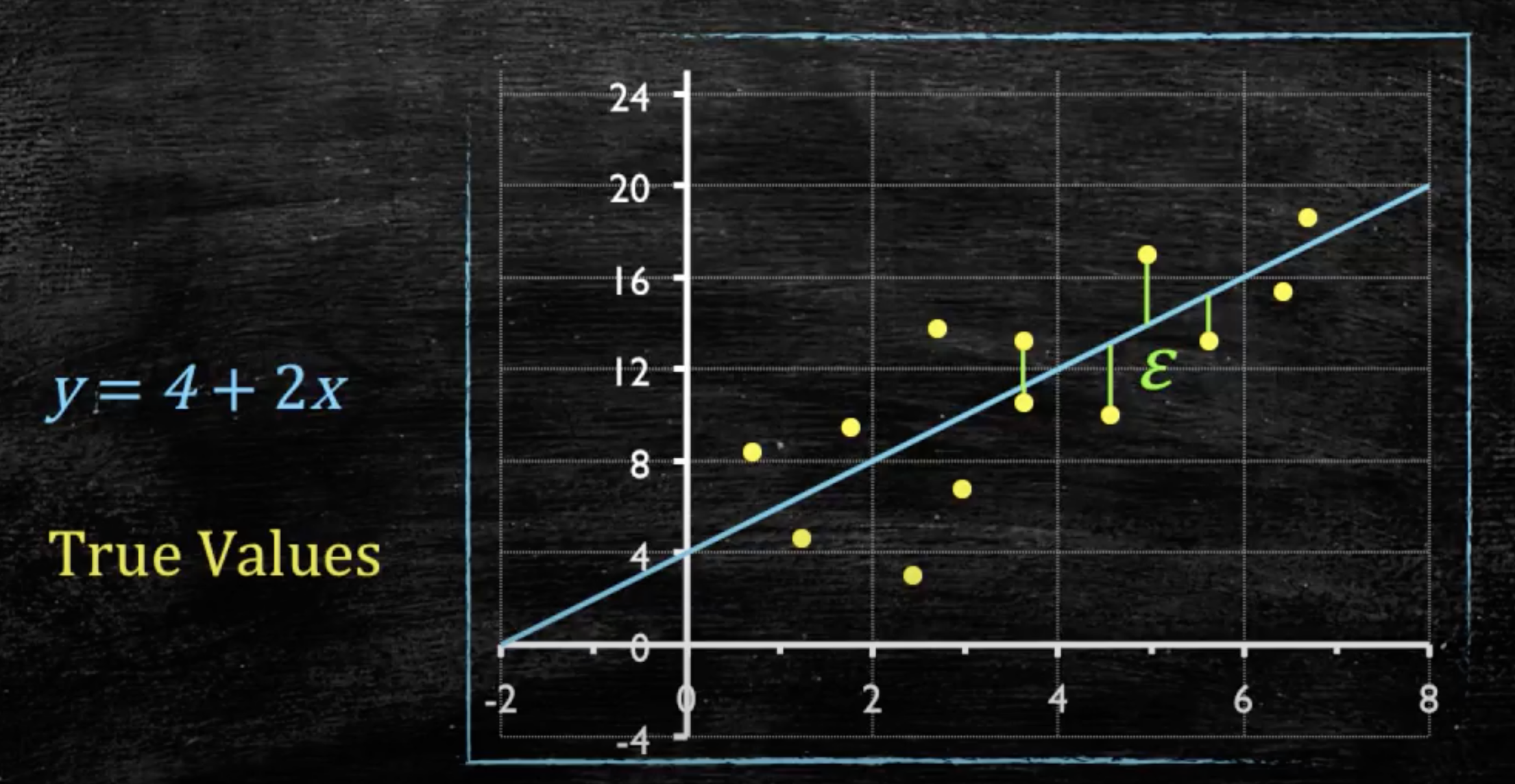
- A leitura sempre será:
- \(\beta_0\): valor estimado de \(y\) quando \(x=0\)
- \(\beta_1\): mudança (aumento ou diminuição) estimada de \(y\) para cada unidade de aumento em \(x\)
Exemplo 1: estimar altura em função da idade
(altura ~ idade)
Exemplo 1: estimar altura em função da idade
(altura ~ idade)
Exemplo 1: estimar altura em função da idade
(altura ~ idade)
Exemplo 1: estimar altura em função da idade
(altura ~ idade)
library(tidyverse)
# Criar dois vetores numéricos e colocá-los num dataframe
idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12)
altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153)
ex1 = data.frame(idade, altura)
# Modelo
modAltura = lm(altura ~ idade, data = ex1)
modAltura
Call:
lm(formula = altura ~ idade, data = ex1)
Coefficients:
(Intercept) idade
62.504 7.545 - A leitura sempre será:
- \(\beta_0\): valor estimado de \(y\) quando \(x=0\)
- \(\beta_1\): mudança (aumento ou diminuição) estimada de \(y\) para cada unidade de aumento em \(x\)
- \(\beta_0 = 62.5\): altura quando idade é zero
- \(\beta_1 = 7.5\): aumento da altura para cada ano a mais na idade
Utilizando os coeficientes para gerar a reta de regressão
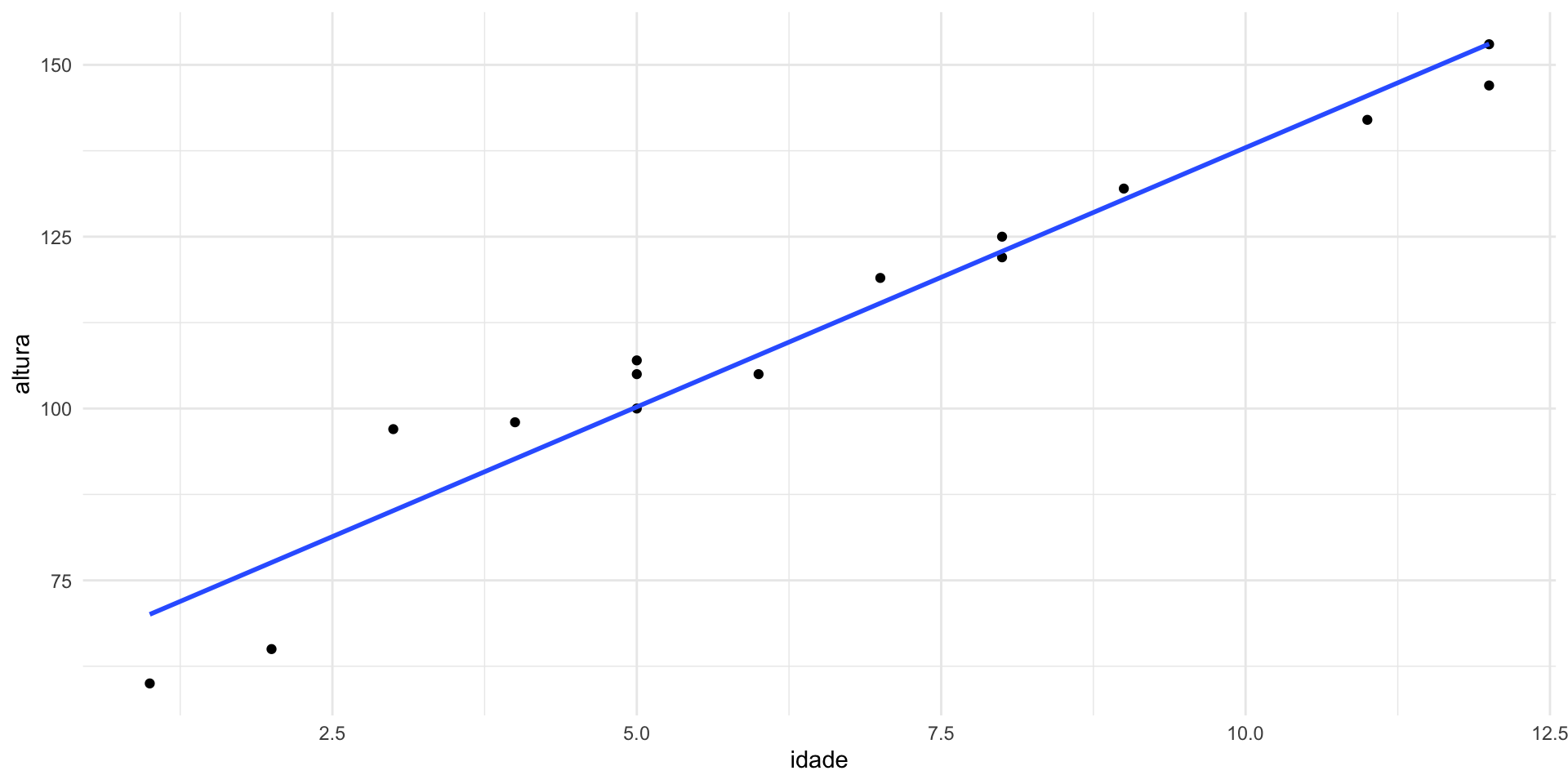
- \(\beta_0\) também é chamado de intercepto (intercept) ou coeficiente linear
- \(\beta_1\) também é chamado de slope ou coeficiente angular
- \(\beta_1\) é o tamanho do efeito!
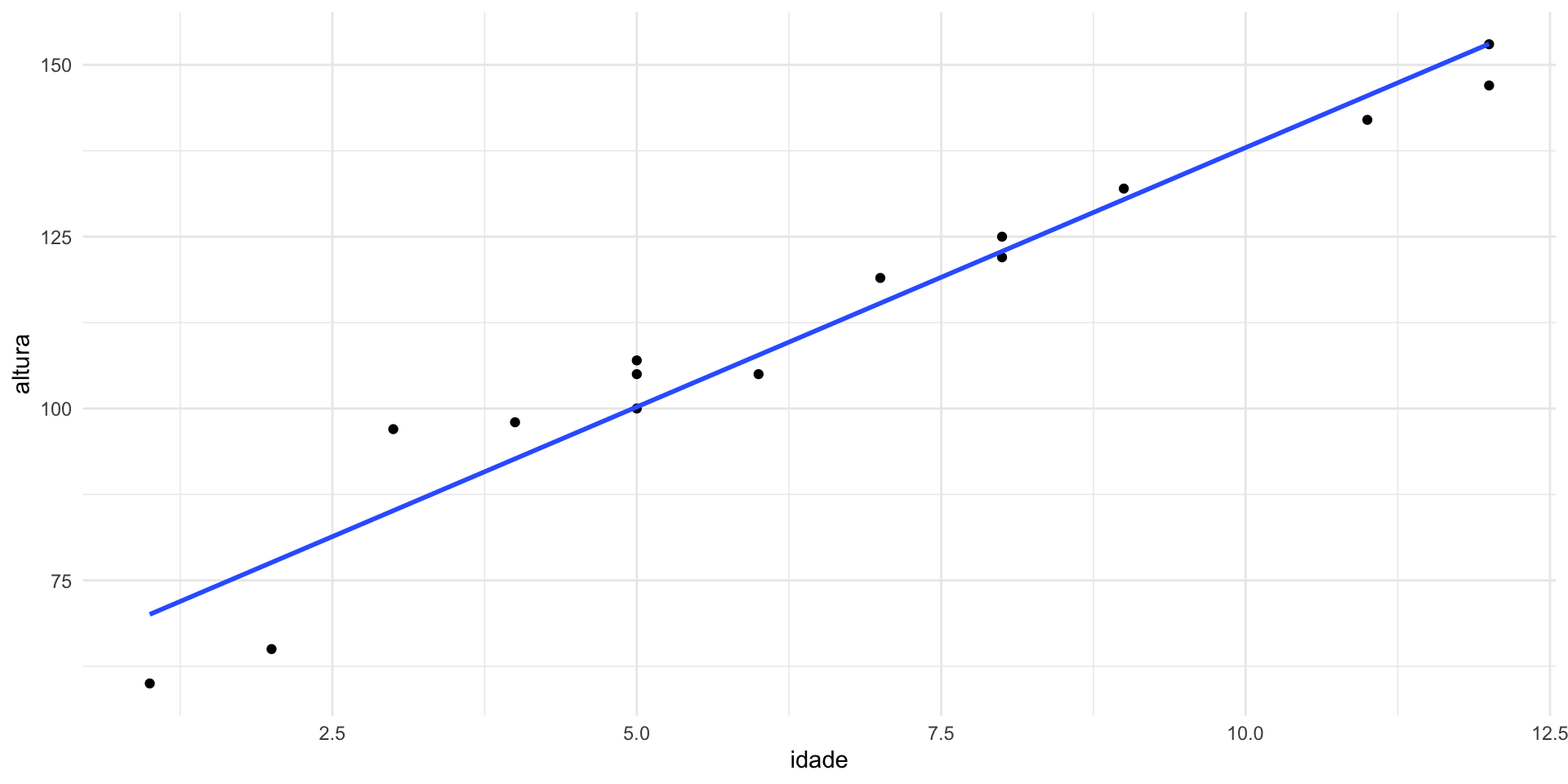
- \(\beta_0 = 62.5\)
- \(\beta_1 = 7.5\)
Prevendo dados não observados
- Lembrando: \(y = \beta_0+\beta_1x\)
- \(\beta_0 = 62.5\)
- \(\beta_1 = 7.5\)
- Logo: \(y = 62.5 + 7.5 \times x\)
- Qual é a altura prevista pelo modelo para alguém de 4 anos de idade?
- \(y = 62.5 + 7.5 \times 4\)
- \(y = 92.5\) (93 centímetros)
- Qual é a altura prevista pelo modelo para alguém de 14 anos de idade?
- \(y = 62.5 + 7.5 \times 14\)
- \(y = 167.5\) (1,68 metro)
Demais informações do modelo
Call:
lm(formula = altura ~ idade, data = ex1)
Residuals:
Min 1Q Median 3Q Max
-12.5946 -3.1391 -0.0477 4.2242 11.8601
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.5040 3.7691 16.58 3.98e-10 ***
idade 7.5453 0.5135 14.69 1.78e-09 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.651 on 13 degrees of freedom
Multiple R-squared: 0.9432, Adjusted R-squared: 0.9388
F-statistic: 215.9 on 1 and 13 DF, p-value: 1.782e-09- Modelo
Resíduos
1 2 3 4 5 6
-10.04928458 -12.59459459 11.86009539 5.31478537 -0.23052464 4.76947536
7 8 9 10 11 12
6.76947536 -2.77583466 3.67885533 -0.86645469 2.13354531 1.58823529
13 14 15
-3.50238474 -6.04769475 -0.04769475 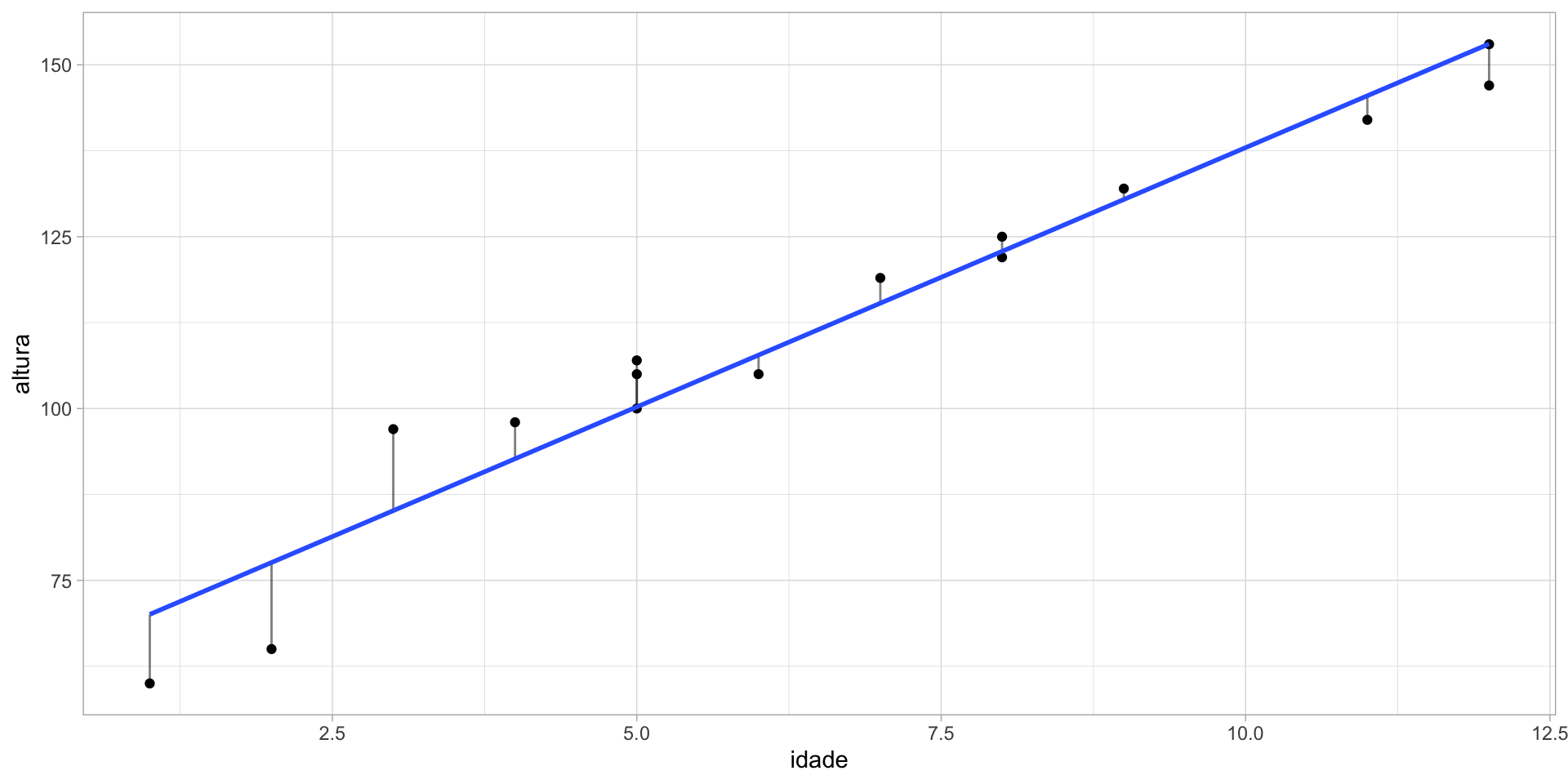
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.5040 3.7691 16.58 3.98e-10 ***
idade 7.5453 0.5135 14.69 1.78e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Estimate: coeficientes estimados (intercept e slope)Std. Error: erro padrão de cada coeficientet value: teste-t para cada coeficiente (\(H_0\) coeficiente \(= 0\))Pr(>|t|): valores de p dos testes-t- O que quer dizer intercepto \(\ne 0\)?
- O que quer dizer slope \(\ne 0\)?
Signif. codes: Níveis de significância sugeridos pelo R
Residual standard error: 6.651 on 13 degrees of freedom
Multiple R-squared: 0.9432, Adjusted R-squared: 0.9388
F-statistic: 215.9 on 1 and 13 DF, p-value: 1.782e-09 - Erro padrão dos resíduos e graus de liberdade
- \(R^{2}\) (\(r\) de Pearson ao quadrado): indica o quanto de variabilidade na variável resposta é explicada pelas variáveis incluídas no modelo
- neste caso, \(94\%\) da altura pode ser explicada/prevista pela idade
- \(R^{2}\) ajustado é um ajuste a depender do número de variáveis preditoras incluídas no modelo (em regressão múltipla)
- Teste-F é utilizado para comparação de modelos (se acrescentar variáveis preditoras melhoram o modelo)
Prevendo mais dados não observados
- \(y = 62.5 + 7.5 \times x\)
- Qual é a altura prevista pelo modelo para um recém-nascido?
- \(y = 62.5 + 7.5 \times 0\)
- \(y = 62.5\) (63 centímetros!!!)
- Qual é a altura prevista pelo modelo para alguém de 60 anos de idade?
- \(y = 62.5 + 7.5 \times 60\)
- \(y = 512.5\) (5,13 metros!!!)
- Por quê?
- Os coeficientes não são valores presentes nos dados, e não são valores do mundo real, são valores do modelo
- “All models are wrong, but some are useful” (George E. P. Box)
- “The Golem of Prague” (Richard McElreath)
- Os dados (tipo, quantidade, variedade, representatividade, etc.) que alimentam/ajustam o modelo (fit the model) farão dele um modelo de estimativa melhor ou pior
- Mas lembre-se: o modelo é apenas um robô e vai te obedecer!
- Se você pedir uma reta, ela vai te dar a melhor reta
O quarteto de Anscombe (1973)
\(\bar{X}\) de x = 9
\(s\) de x = 3,3
\(\bar{X}\) de y = 7,5
\(s\) de y = 2
Corr de x e y = 0,816
Regressão linear: \(y = 3+0,5x\)
\(R^2=0,67\)
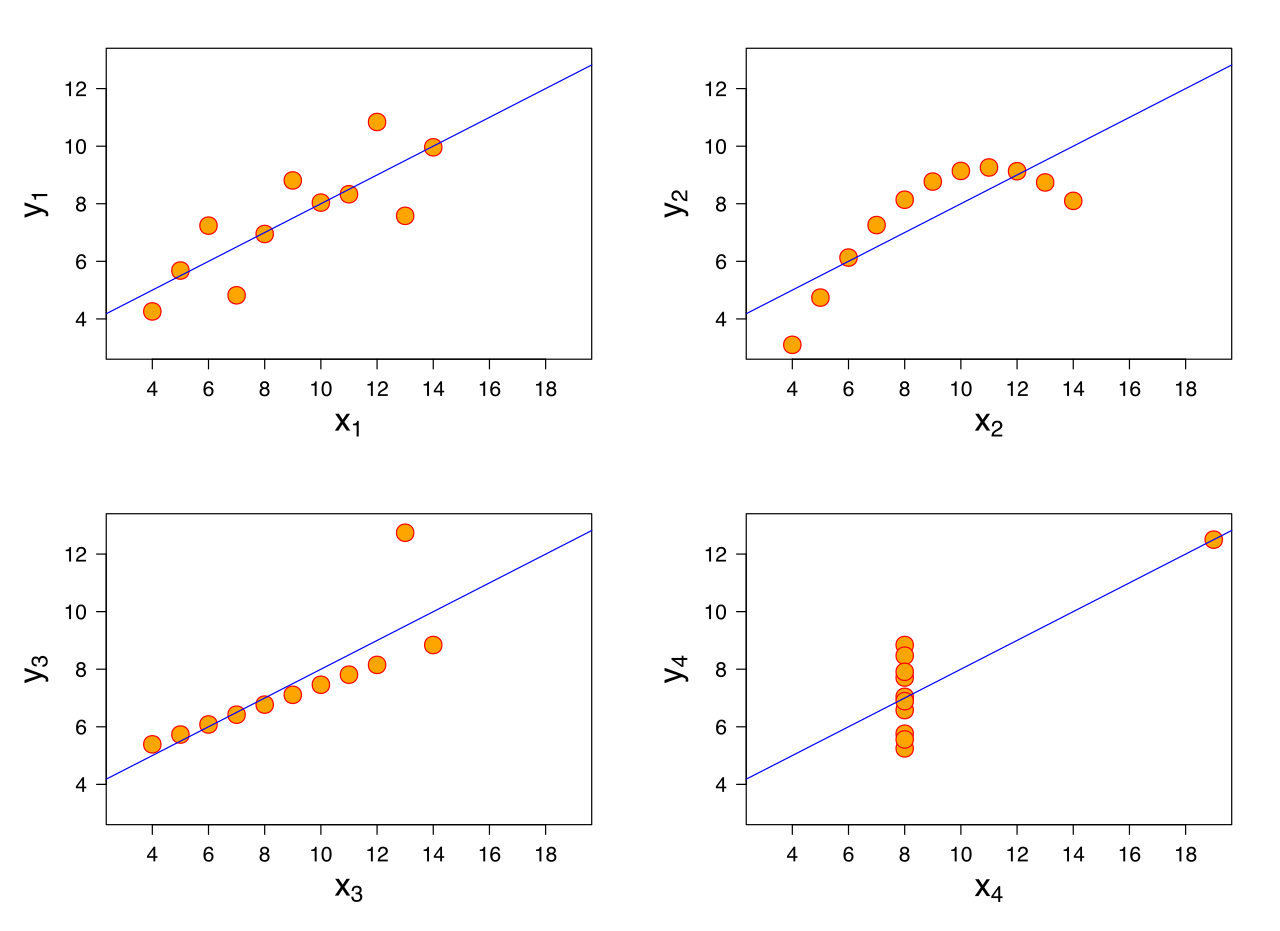
E se acrescentarmos dados de adultos ao nosso modelo de altura?
idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12,
17, 18, 19 ,22, 25, 26, 26, 28, 31, 32, 32, 35, 38, 40, 41, 45, 50,
55, 61, 62, 62, 63)
altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153,
170, 175, 168, 165, 180, 176, 171, 169, 181, 185, 175, 160, 170, 168, 170,
182, 177, 170, 172, 165, 166, 160)
ex2 = data.frame(idade, altura)
# Modelo
modAltura2 = lm(altura ~ idade, data = ex2)
modAltura2
# Visualizar linha de regressão
ggplot(data = ex2, aes(x = idade, y = altura)) +
geom_point() +
geom_smooth(method = lm, se = F)
Call:
lm(formula = altura ~ idade, data = ex2)
Coefficients:
(Intercept) idade
115.918 1.256 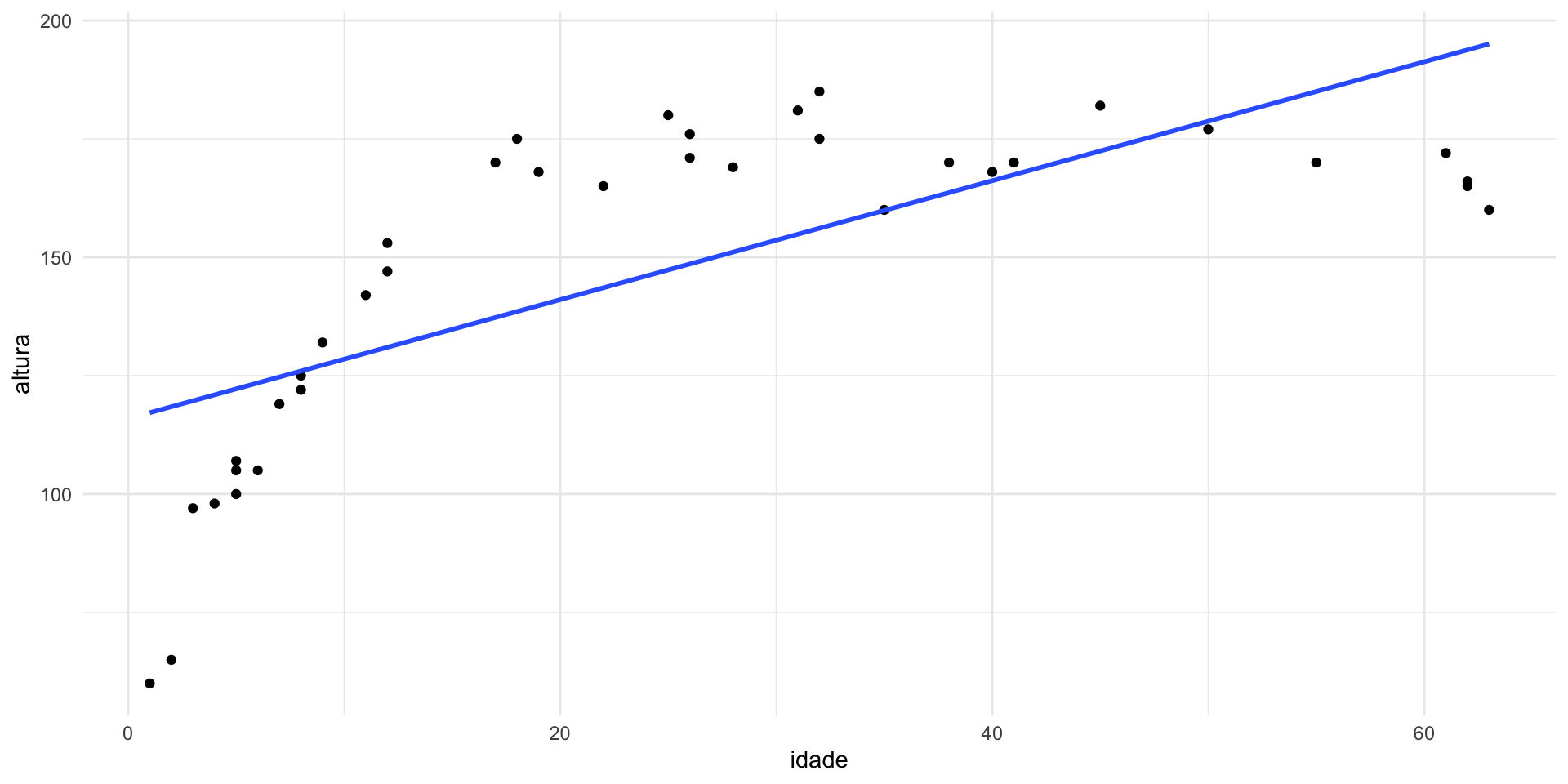
- Se você pedir uma reta, o modelo vai gerar uma reta!
- Nosso modelo certamente não serve para dados de adultos
- O que fazer?
Exemplo Linguístico 1
Modelo com previsor numérico
- Dados
englishdo pacotelanguageR- Dados de tempo de reação (em log) de decisão lexical de 2284 substantivos e verbos do inglês com 34 variáveis preditoras sociais e linguísticas
- Estimar o tempo de reação em função da familiaridade com a palavra
Modelo com previsor numérico
- Dados
englishdo pacotelanguageR- Dados de tempo de reação de decisão lexical de 2284 substantivos e verbos do inglês com 34 variáveis preditoras sociais e linguísticas
- Estimar o tempo de reação em função da familiaridade com a palavra
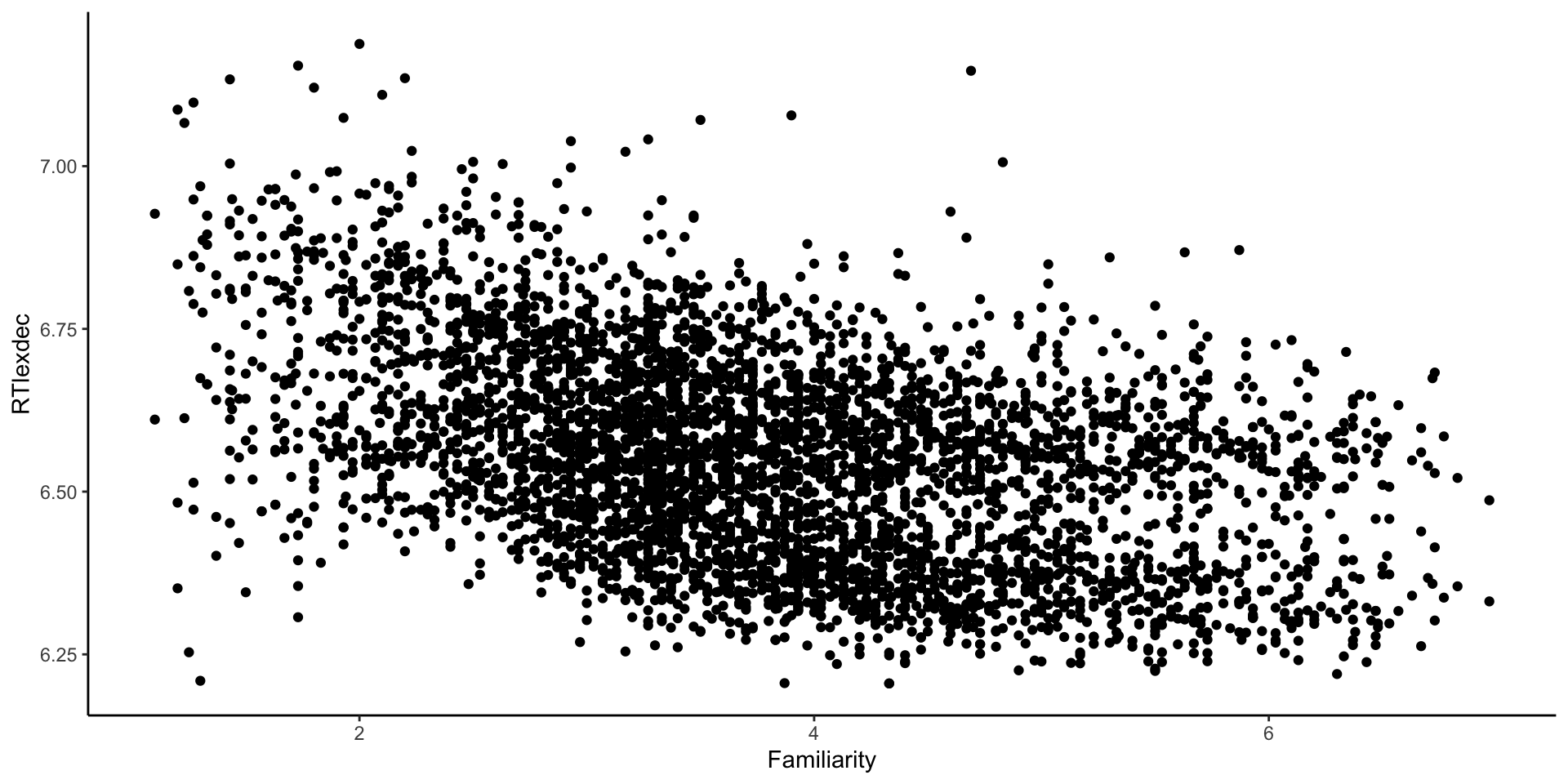
- Conseguem ver alguma associação/correlação?
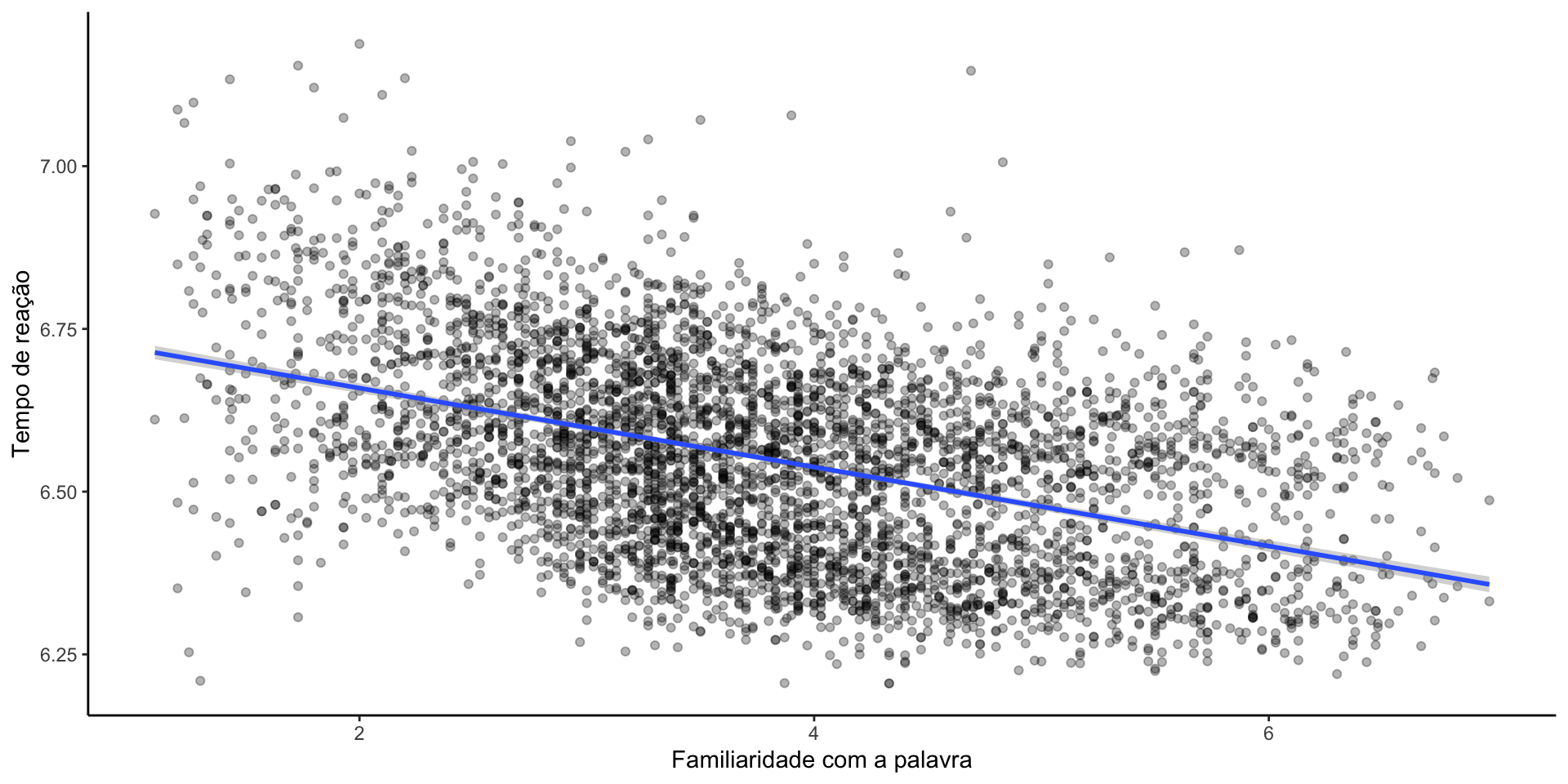
Estimar tempo de reação em função da familiaridade com a palavra
Call:
lm(formula = RTlexdec ~ Familiarity, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.49212 -0.11285 -0.00596 0.10569 0.65072
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.780397 0.007178 944.59 <2e-16 ***
Familiarity -0.060676 0.001810 -33.52 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1406 on 4566 degrees of freedom
Multiple R-squared: 0.1975, Adjusted R-squared: 0.1973
F-statistic: 1124 on 1 and 4566 DF, p-value: < 2.2e-16Estimar tempo de reação em função da familiaridade com a palavra
Call:
lm(formula = RTlexdec ~ Familiarity, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.49212 -0.11285 -0.00596 0.10569 0.65072
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.780397 0.007178 944.59 <2e-16 ***
Familiarity -0.060676 0.001810 -33.52 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1406 on 4566 degrees of freedom
Multiple R-squared: 0.1975, Adjusted R-squared: 0.1973
F-statistic: 1124 on 1 and 4566 DF, p-value: < 2.2e-16- O que quer dizer o intercepto (\(\beta_0\)) de \(6.78\)?
- O que quer dizer o slope (\(\beta_1\)) de \(-0.06\)?
- Qual é o poder explicativo deste modelo?
Exemplo Linguístico 2
Modelo com previsor categórico
- Dados
englishdo pacotelanguageR- Estimar o tempo de reação em função da faixa etária dos participantes (codificada nos dados em
oldeyoung) - Qual seria a hipótese lógica?
- Estimar o tempo de reação em função da faixa etária dos participantes (codificada nos dados em
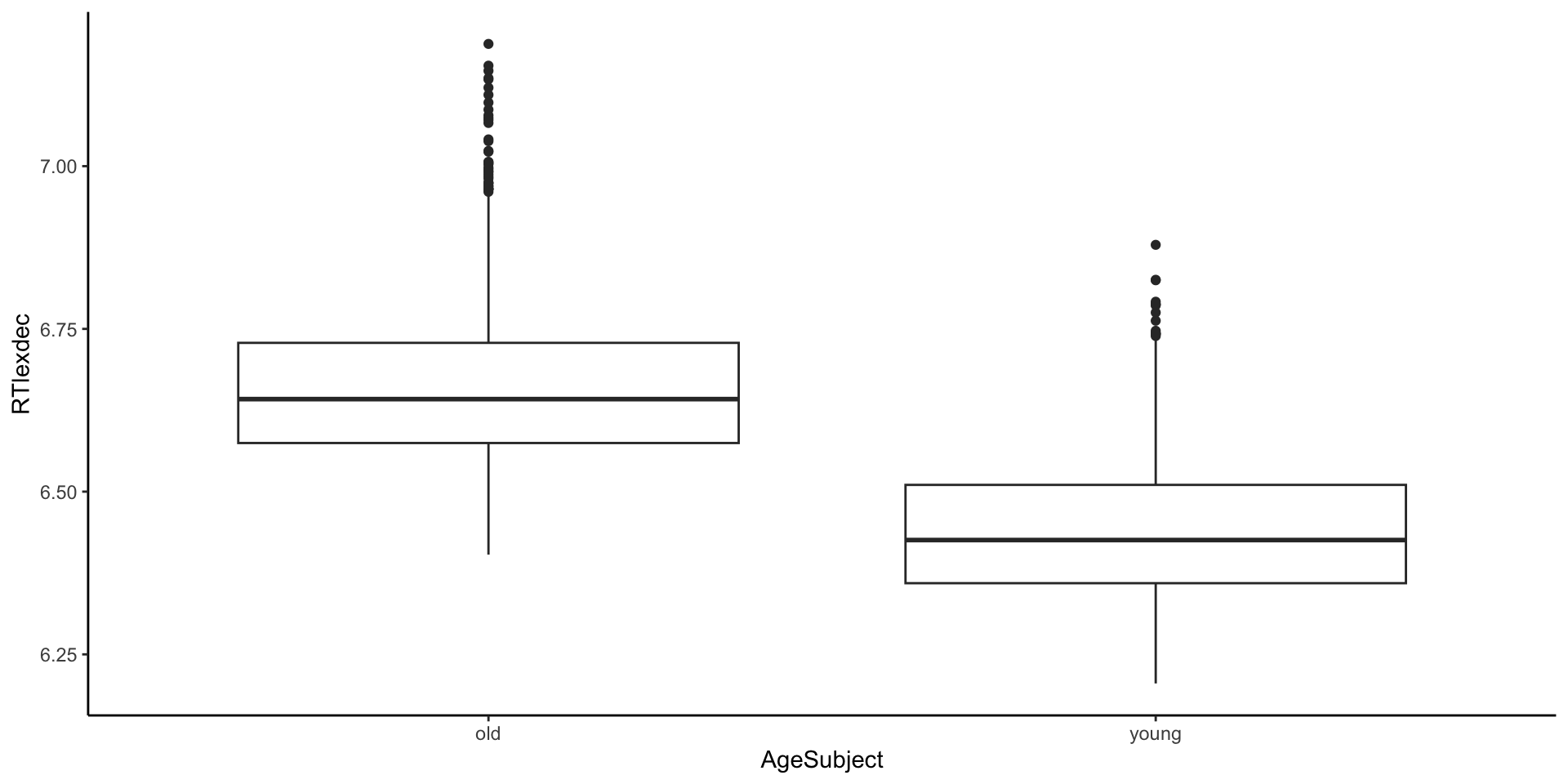
Estimar tempo de reação em função da faixa etária
Call:
lm(formula = RTlexdec ~ AgeSubject, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.25776 -0.08339 -0.01669 0.06921 0.52685
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.660958 0.002324 2866.44 <2e-16 ***
AgeSubjectyoung -0.221721 0.003286 -67.47 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1111 on 4566 degrees of freedom
Multiple R-squared: 0.4992, Adjusted R-squared: 0.4991
F-statistic: 4552 on 1 and 4566 DF, p-value: < 2.2e-16Estimar tempo de reação em função da faixa etária
Call:
lm(formula = RTlexdec ~ AgeSubject, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.25776 -0.08339 -0.01669 0.06921 0.52685
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.660958 0.002324 2866.44 <2e-16 ***
AgeSubjectyoung -0.221721 0.003286 -67.47 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1111 on 4566 degrees of freedom
Multiple R-squared: 0.4992, Adjusted R-squared: 0.4991
F-statistic: 4552 on 1 and 4566 DF, p-value: < 2.2e-16- O que quer dizer o intercepto (\(\beta_0\)) de \(6.66\)?
- O que quer dizer o slope (\(\beta_1\)) de \(-0.22\)?
- Qual é o poder explicativo deste modelo?
Momento mão na massa!
Slides / códigos:

Tarefa 1:
- Usando os dados
englishdo pacotelanguageR:- estime o tempo de reação (
RTlexdec) em função da frequência escrita da palavra (WrittenFrequency) - Gere um gráfico que mostre a relação entre essas variáveis
- estime o tempo de reação (
- Antes de ajustar o modelo:
- qual seria a hipótese lógica?
- Após ajustar o modelo:
- Qual é o valor de \(\beta_0\)? O que ele representa?
- Qual é o valor de \(\beta_1\)? O que ele representa?
- O modelo prevê um efeito de frequência escrita da palavra sobre o tempo de reação?
- Qual é o poder explicativo do modelo?
Tarefa 2:
- Usando os dados
englishdo pacotelanguageR:- estime o tempo de reação (
RTlexdec) em função da categoria da palavra (WordCategory), se verbo ou substantivo (codificados emVeN) - Gere um gráfico que mostre a relação entre essas variáveis
- estime o tempo de reação (
- Antes de ajustar o modelo:
- há uma hipótese lógica?
- Após ajustar o modelo:
- Qual é o valor de \(\beta_0\)? O que ele representa?
- Qual é o valor de \(\beta_1\)? O que ele representa?
- O modelo prevê um efeito de ser substantivo ou verbo sobre o tempo de reação?
- Qual é o poder explicativo do modelo?
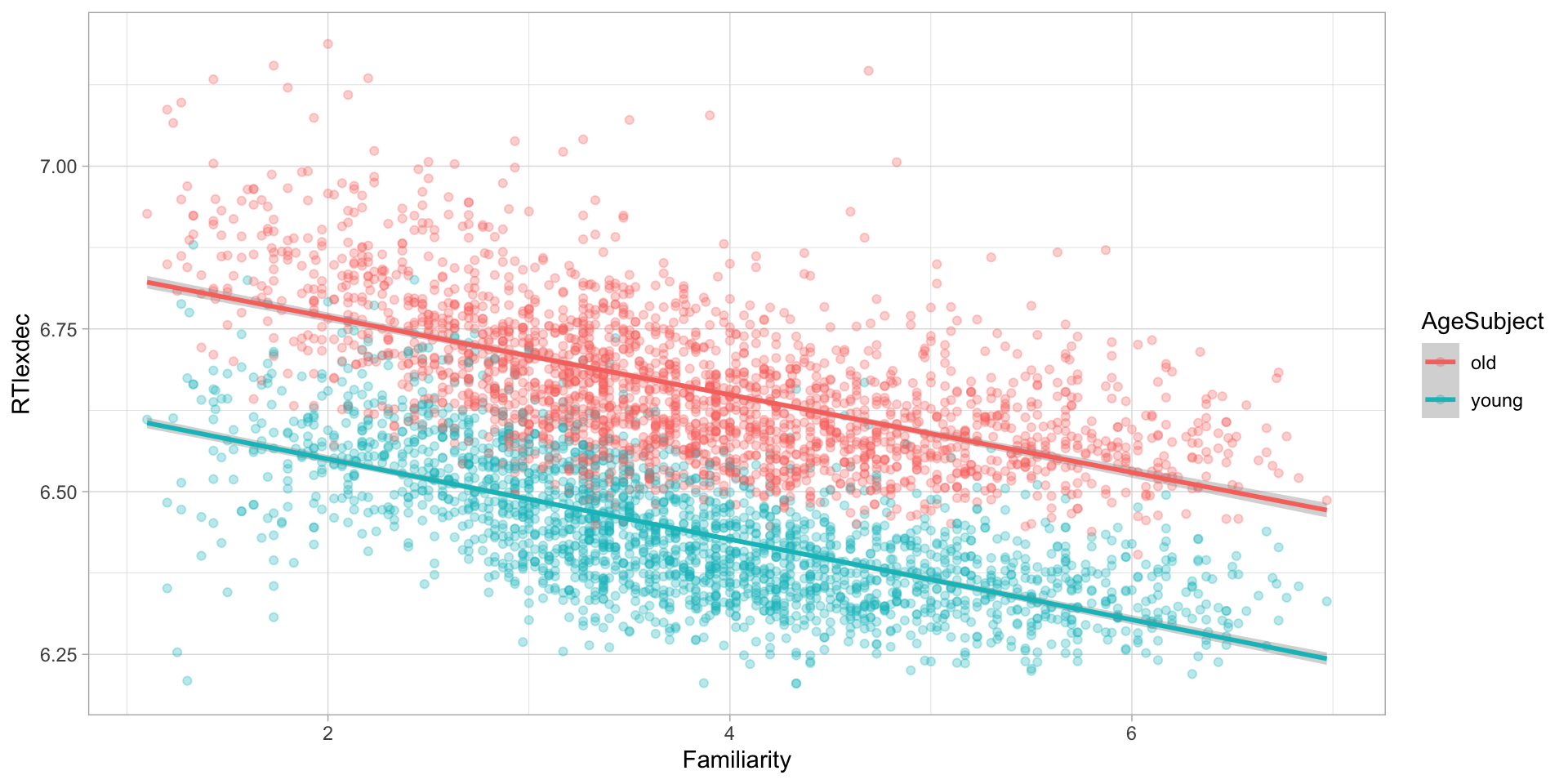
Regressão Linear Múltipla
Nos dados english vimos o efeito de familiaridade com a palavra e o de faixa etária sobre o tempo de reação em modelos separados:
E se juntarmos as duas variáveis preditoras no mesmo modelo?
- Regressão Linear Múltipla
- se na simples tínhamos \(y = \beta_0+\beta_1x\)
- na múltipla temos \(y = \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3...\)
- no nosso caso: \(tempoReção = \beta_0+\beta_1\times idade +\beta_2\times familiaridade\)
- forneceremos vários valores de tempo de reação, idade e familiaridade, e queremos que o modelo estime \(\beta_0\) e \(\beta_1\)
“we live in a multifactorial world in which probably no phenomenon is really monofactorial – probably just about everything is correlated with several things at the same time”. (Gries, Stefan Th 2013)
Como visualizar as associações das três variáveis em um mesmo gráfico?
Modelo
Call:
lm(formula = RTlexdec ~ Familiarity + AgeSubject, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.38126 -0.05907 -0.00418 0.05134 0.53986
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.891258 0.004595 1499.82 <2e-16 ***
Familiarity -0.060676 0.001113 -54.52 <2e-16 ***
AgeSubjectyoung -0.221721 0.002558 -86.69 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08643 on 4565 degrees of freedom
Multiple R-squared: 0.6967, Adjusted R-squared: 0.6966
F-statistic: 5244 on 2 and 4565 DF, p-value: < 2.2e-16Modelo
Call:
lm(formula = RTlexdec ~ Familiarity + AgeSubject, data = english)
Residuals:
Min 1Q Median 3Q Max
-0.38126 -0.05907 -0.00418 0.05134 0.53986
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.891258 0.004595 1499.82 <2e-16 ***
Familiarity -0.060676 0.001113 -54.52 <2e-16 ***
AgeSubjectyoung -0.221721 0.002558 -86.69 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.08643 on 4565 degrees of freedom
Multiple R-squared: 0.6967, Adjusted R-squared: 0.6966
F-statistic: 5244 on 2 and 4565 DF, p-value: < 2.2e-16- Como interpretar:
- \(\beta_0\)?
- \(\beta_1\)?
- \(\beta_2\)?
- \(\hat{R}\)?
- Qual é o tempo de reação estimado pelo modelo de um velho a uma palavra de familiaridade 1?
- E de um jovem a uma palavra de familiaridade 4?
Comparação dos modelos
- É melhor ajustar e reportar os 2 modelos simples separadamente ou o modelo múltiplo?
- Um valor de F maior indica que incluir as variáveis melhorou o poder explicativo do modelo
- Podemos rodar
anova(modelo1, modelo2)para comparar estatisticamente os valores de F (p<0.05indica que o modelo mais complexo é superior)
Podemos incluir quantas variáveis preditoras em um modelo de regressão?
- Tantas quanto …? Tivermos? Quisermos? Forem necessárias/motivadas/coerentes/lógicas?
- Atenção:
- Navalha de Occam
- Multicolinearidade
- Interação
- Pensar/Modelar possíveis relações de causalidade antes (remover variáveis de confusão) \(\rightarrow\) DAGs
Mais mão na massa!
Slides / códigos:

Tarefa 3:
- Usando os dados
englishdo pacotelanguageR:- estime o tempo de reação (
RTlexdec) em função da familiaridade com a palavra (Familiarity) + faixa etária (AgeSubject) + frequência escrita da palavra (WrittenFrequency) - interprete os coeficientes e verifique o poder explicativo do modelo
- Desafio: Como gerar um gráfico que mostre a relação das 4 variáveis?
- estime o tempo de reação (
Tarefa 4:
- Acrescente ao modelo anterior a variável categoria da palavra (
WordCategory)- interprete os coeficientes e verifique o poder explicativo do modelo
- Compare a significância de
WordCategoryquando estava em um modelo simples com sua significância neste modelo - Compare o poder explicativo deste modelo ao do anterior
- Bônus: podemos usar
anova(modelo1, modelo2)para comparar modelos (p<0.05indica que o modelo mais complexo é superior)