# Análise quantitativa de dados na Linguística {background-color="#40666e"} ## Séc. XX $\rightarrow$ Estruturalismo e Gerativismo - Objeto da Linguística como estrutura invariável, sistema de oposições, inato, discreto e categórico - Levou a introspecção e dados/exemplos autocunhados > "*Large groups of people make up all their utterances out of the same stock of lexical forms and grammatical constructions. A linguistic observer therefore can describe the speech-habits of a community **without resorting to statistics.***" (Bloomfield 1935: 37) ## Séc. XX $\rightarrow$ Estruturalismo e Gerativismo - Objeto da Linguística como estrutura invariável, sistema de oposições, inato, discreto e categórico - Levou a introspecção e dados/exemplos autocunhados > "*I think we are forced to conclude that grammar is autonomous and independent of meaning, and that **probabilistic models give no particular insight into some of the basic problems of syntactic structure.***" (Chomsky 1957: 17) ## Hoje - Abordagens baseadas no uso, variação e mudança - Dados de corpora, questionários, experimentos, correlatos físicos, construtos da psicologia, etc. . . . - psicolinguística, linguística de corpus, fonética/fonologia, sociolinguística, linguística aplicada, aquisição de L2, linguística forense, aprendizagem de máquinas, etc. - e mesmo subáreas "tradicionais" que não utilizavam (sintaxe, fonologia, etc.) . . . - Como saber se \emph{uma diferença} de 3%, 5%, 8%, 10%, etc. na fala de pessoas de dois estados, de duas faixas etárias, etc. é **aleatória** ou **efeito**? ## Objetivos da Análise Quantitativa de Dados - Descrever - Explicar - Prever # Antes da Coleta de Dados {background-color="#40666e"} ## Problema $\rightarrow$ Pergunta(s) $\rightarrow$ Hipótese(s) $\rightarrow$ Verificar/Observar/Testar $\rightarrow$ Inferência/Conclusão . . . - Ex. 1: encontrar o melhor preço para um produto - Ex. 2: motivos de lentidão em um novo percurso ## Passos **ANTES** da coleta de dados ::: incremental - identificar/caracterizar o problema - estudar a literatura (teoria, construtos, métodos, resultados, variáveis, lacunas, etc.) - observar o fenômeno e raciocínio dedutivo por parte do pesquisador - compilar variáveis passíveis de influência - estipular hipóteses - falsiáveis e testáveis - H1 e H0 (somadas devem abarcar todos possíveis resultados) ::: ## Passos **ANTES** da coleta de dados ::: incremental - identificar/vislumbrar variáveis de confusão - pensar nas direções das possíveis causalidades - pensar em como operacionalizar as variáveis (observar, medir, contar) - medir errado não tem conserto! - pensar em amostras equilibradas e o mais randomizada possível ::: ## Problemas de operacionalização Devemos desenvolver uma rotina de racioncínio questionador ::: incremental - "Ação com gêmeos idênticos mostra que mascar chiclete dá uma boa impressão" - *The stuff of thought* (Steven Pinker) - "Pesquisa mostra que correr pode ser prejudicial a saúde" - *HARKing* ::: # Análise Quantitativa de Dados {background-color="#40666e"} ## O que não faremos: - Testes de Hipótese (*Null-Significance Hypothesis Testing*): - Teste de Proporção e Qui-quadrado - Teste-t - Teste de correlação - ANOVA - Testes não paramétricos - Wilcoxon - Kruskal-Wallis - Friedman - Spearman ## Por quê? 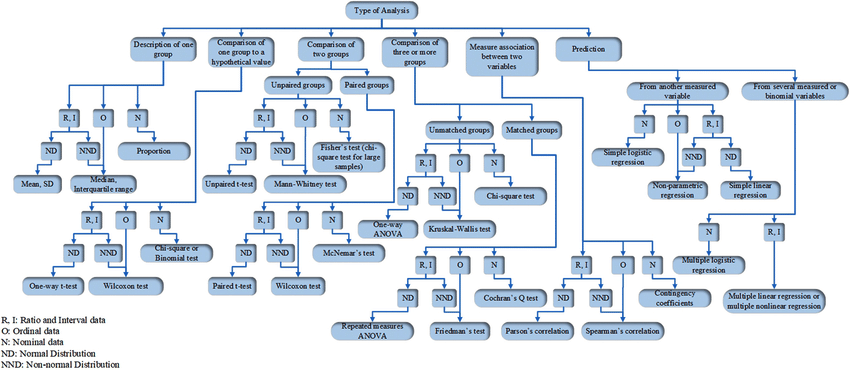{} ## O que faremos? Modelos de Regressão :::incremental - Utilizáveis para qualquer tipo de dado/desenho experimental - linear, logístico, ordinal, *poisson*, multinominal - Exige menos requisitos (*assumptions*) dos dados - O resultado já é o tamanho do efeito - Informa por padrão o poder explicativo do modelo - pode incorporar interações e efeitos mistos ::: # Princípios básicos de regressão {background-color="#40666e"} ## Precisamos partir de uma correlação {} ## Possíveis associações entre variáveis: {} ## - Correlação é um requisito para regressão - Precisa haver associação entre variáveis para haver efeito . . . - Porém - correlação não implica motivação - *correlation does not mean causation* ## 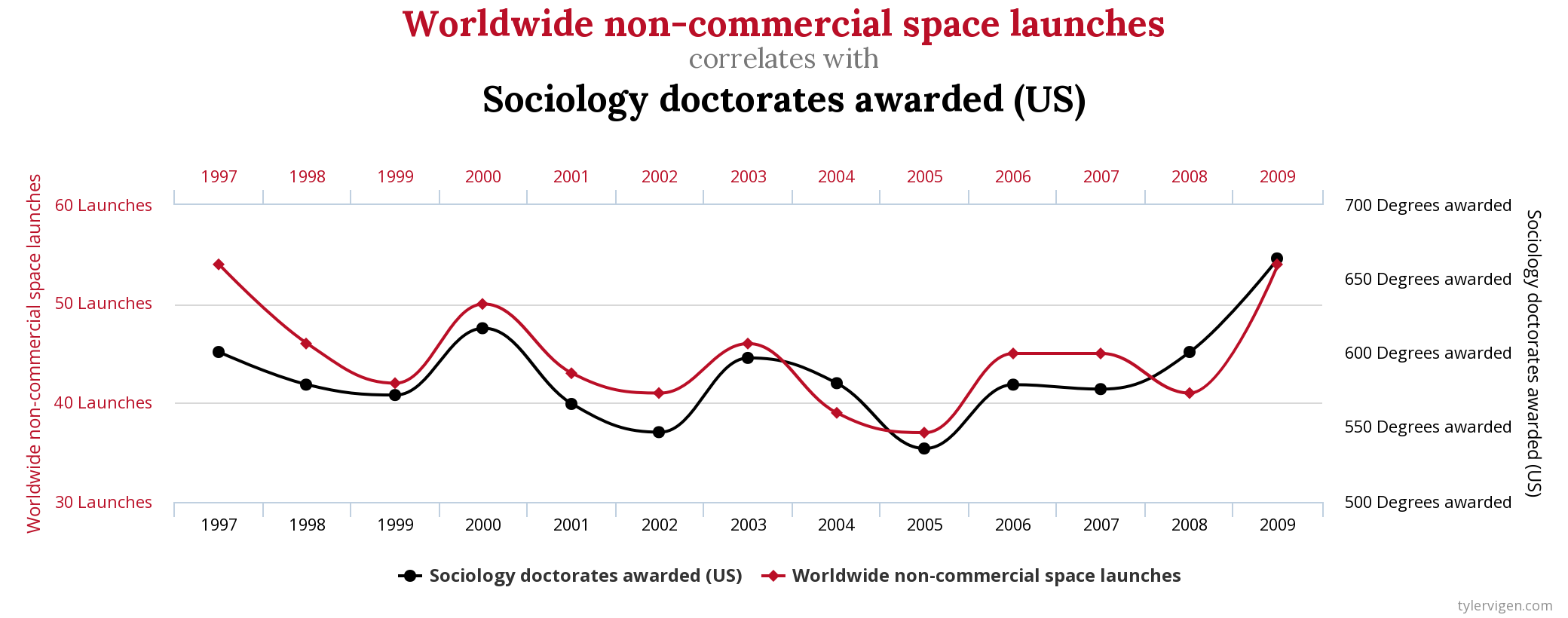{fig-align="center"} ## 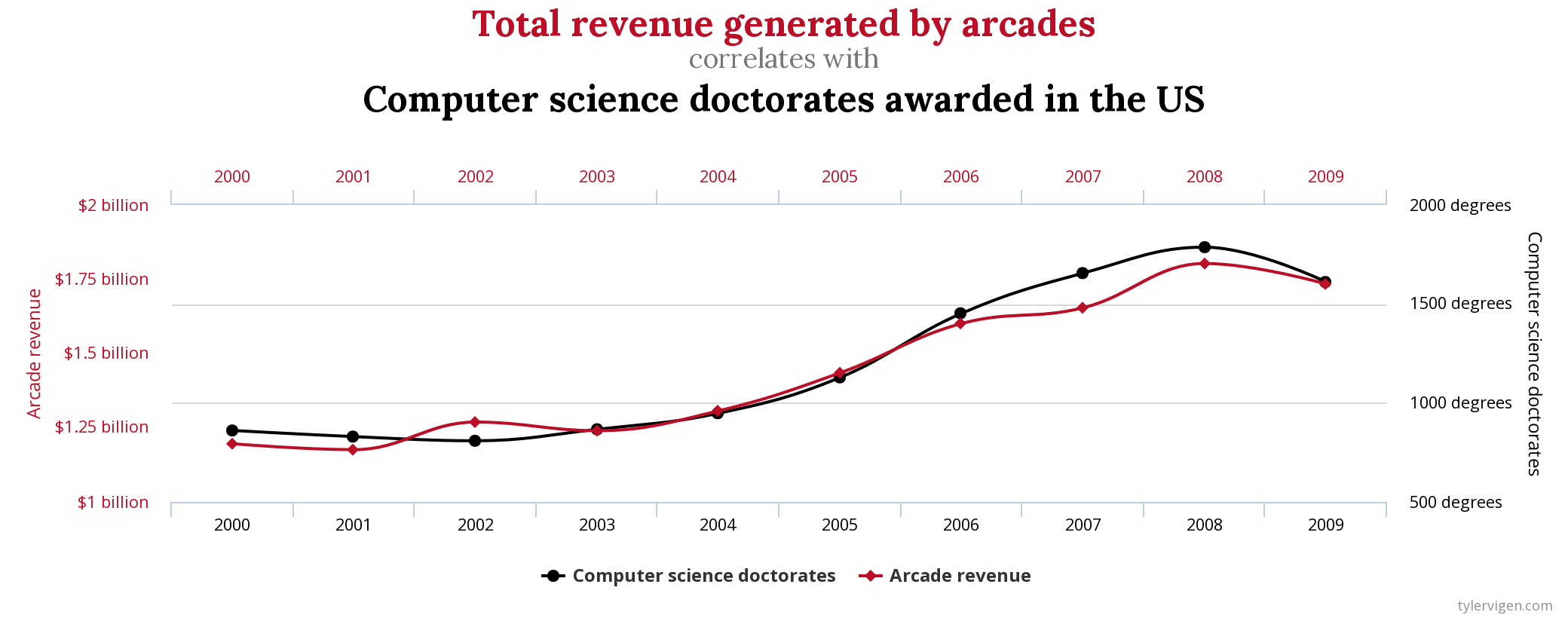{fig-align="center"} ## 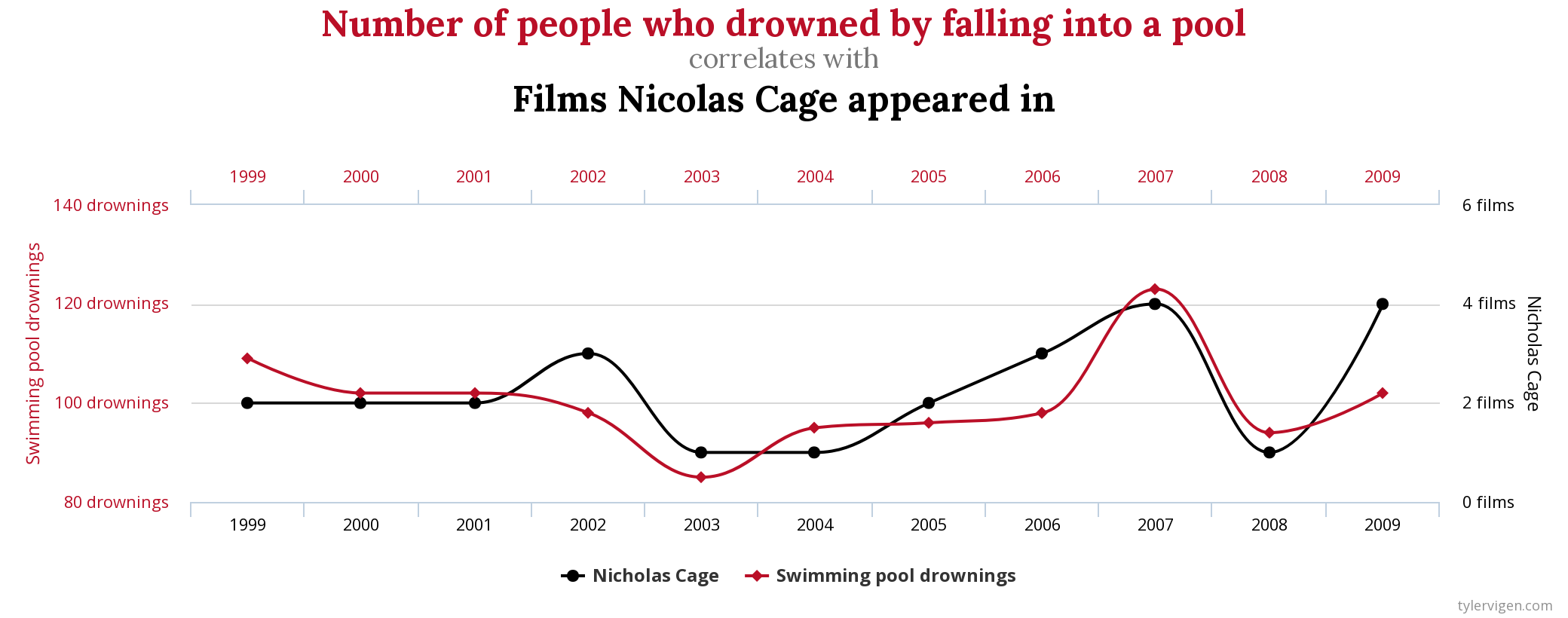{fig-align="center"} ## 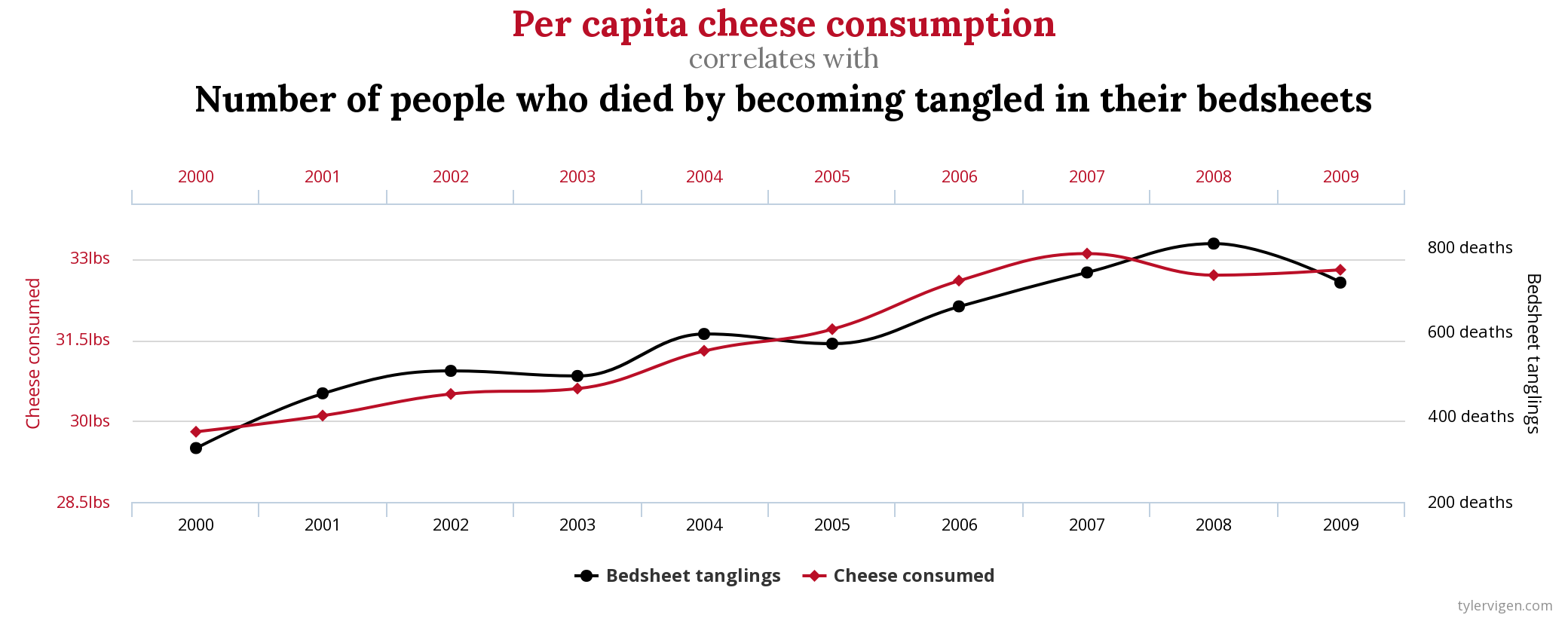{fig-align="center"} ## Objetivos - Verificar se há uma relação entre variáveis - Correlação e regressão - Prever valores não observados - Regressão # Regressão Linear Simples {background-color="#40666e"} ## - Modelos de Regressão estimam o valor de $y$ baseado no valor de $x$ - $y =$ variável de resposta (variável dependente) - $x =$ variável preditora (variável independente) {} ## Modelo de Regressão **Linear Simples** - **Linear**: a variável de resposta deve ser numérica (contínua) - **Simples**: apenas uma variável preditora - pode ser numérica ou categórica ## Modelo de Regressão **Linear Simples** - Estima-se o valor de $y$ em função do valor de $x$ - $y$ ~ $x$ . . . - Para desenhar a reta de regressão, utilizamos a equação linear - $y = a+bx$ - $y = \beta_0+\beta_1x$ . . . - $y$ é o valor a ser estimado -- variável de resposta - $x$ é o valor em função do qual a estimação será feita -- variável preditora - $\beta_0$ e $\beta_1$ são coeficientes fornecidos pelo modelo - $\beta_0$ diz onde a reta começa - $\beta_1$ diz o ângulo da reta ## {} [https://www.youtube.com/watch?v=owI7zxCqNY0](https://www.youtube.com/watch?v=owI7zxCqNY0) ## {} [https://www.youtube.com/watch?v=owI7zxCqNY0](https://www.youtube.com/watch?v=owI7zxCqNY0) ## {} [https://www.youtube.com/watch?v=owI7zxCqNY0](https://www.youtube.com/watch?v=owI7zxCqNY0) ## {} [https://www.youtube.com/watch?v=owI7zxCqNY0](https://www.youtube.com/watch?v=owI7zxCqNY0) ## - Coletamos dados $\rightarrow$ informamos dados ao modelo (vários valores de $x$ e de $y$) $\rightarrow$ modelo calcula $\beta_0$ e $\beta_1$ e desenha a reta $\rightarrow$ usamos a reta para prever valores não observados ::: columns ::: {.column width="70%"} {height=4in} [https://www.youtube.com/watch?v=owI7zxCqNY0](https://www.youtube.com/watch?v=owI7zxCqNY0) ::: ::: {.column width="30%"} - valor observado $-$ valor estimado $=$ resíduo - o modelo desenha uma reta gerando os menores resíduos possíveis ::: ::: ## {height=3in} - A leitura sempre será: - $\beta_0$: valor **estimado** de $y$ quando $x=0$ - $\beta_1$: mudança (aumento ou diminuição) **estimada** de $y$ para cada unidade de aumento em $x$ ## Exemplo 1: estimar altura em função da idade{auto-animate="true"} ### (altura ~ idade) ```r library(tidyverse) ``` ## Exemplo 1: estimar altura em função da idade{auto-animate="true"} ### (altura ~ idade) ```r library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153) ``` ## Exemplo 1: estimar altura em função da idade{auto-animate="true"} ### (altura ~ idade) ```r library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153) ex1 = data.frame(idade, altura) ``` ## Exemplo 1: estimar altura em função da idade{auto-animate="true"} ### (altura ~ idade) ```r library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153) ex1 = data.frame(idade, altura) # Modelo modAltura = lm(altura ~ idade, data = ex1) modAltura ``` ```{r} library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153) ex1 = data.frame(idade, altura) # Modelo modAltura = lm(altura ~ idade, data = ex1) modAltura ``` ## ```{r} #| echo: true modAltura = lm(altura ~ idade, data = ex1) modAltura ``` . . . - A leitura sempre será: - $\beta_0$: valor **estimado** de $y$ quando $x=0$ - $\beta_1$: mudança (aumento ou diminuição) **estimada** de $y$ para cada unidade de aumento em $x$ . . . - $\beta_0 = 62.5$: altura quando idade é zero - $\beta_1 = 7.5$: aumento da altura para cada ano a mais na idade ## Utilizando os coeficientes para gerar a reta de regressão ```r ggplot(data = ex1, aes(x = idade, y = altura)) + geom_point() + geom_smooth(method = lm, se = F) ``` ```{r} library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153) ex1 = data.frame(idade, altura) # Visualizar a distribuição ggplot(data = ex1, aes(x = idade, y = altura)) + geom_point() + geom_smooth(method = lm, se = F) + theme_minimal() ``` ## - $\beta_0$ também é chamado de **intercepto (*intercept*)** ou **coeficiente linear** - $\beta_1$ também é chamado de ***slope*** ou **coeficiente angular** - $\beta_1$ é o [tamanho do efeito]{.fg style="--col: #e64173"}! ```{r} ggplot(data = ex1, aes(x = idade, y = altura)) + geom_point() + geom_smooth(method = lm, se = F) + theme_minimal() ``` - $\beta_0 = 62.5$ - $\beta_1 = 7.5$ ## Prevendo dados não observados - Lembrando: $y = \beta_0+\beta_1x$ - $\beta_0 = 62.5$ - $\beta_1 = 7.5$ - Logo: $y = 62.5 + 7.5 \times x$ ::: incremental - Qual é a altura prevista pelo modelo para alguém de 4 anos de idade? - $y = 62.5 + 7.5 \times 4$ - $y = 92.5$ (93 centímetros) - Qual é a altura prevista pelo modelo para alguém de 14 anos de idade? - $y = 62.5 + 7.5 \times 14$ - $y = 167.5$ (1,68 metro) ::: ## Demais informações do modelo ```{r} #| echo: true #| output-location: fragment summary(modAltura) ``` ## ```{code-block-bg: true} Call: lm(formula = altura ~ idade, data = cor) ``` - Modelo . . . ```{code-block-bg: true} Residuals: Min 1Q Median 3Q Max -12.5946 -3.1391 -0.0477 4.2242 11.8601 ``` - Distribuição dos resíduos - inspecione visualmente se os resíduos estão minimamente simétricos - se o modelo erra, melhor que erre tanto para mais como para menos ## Resíduos ```r modAltura$residuals ``` ```{r} modAltura$residuals ex1$predicted <- predict(modAltura) ex1$residuals <- residuals(modAltura) ggplot(ex1, aes(x = idade, y = altura)) + geom_segment(aes(xend = idade, yend = predicted), alpha = .5) + geom_point() + geom_smooth(method = lm, se = F) + theme_light() ``` ## ```{code-block-bg: true} Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 62.5040 3.7691 16.58 3.98e-10 *** idade 7.5453 0.5135 14.69 1.78e-09 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ``` ::: incremental - `Estimate`: coeficientes estimados (*intercept* e *slope*) - `Std. Error`: erro padrão de cada coeficiente - `t value`: teste-t para cada coeficiente ($H_0$ coeficiente $= 0$) - `Pr(>|t|)`: valores de *p* dos testes-t - O que quer dizer intercepto $\ne 0$? - O que quer dizer slope $\ne 0$? - `Signif. codes`: Níveis de significância sugeridos pelo R ::: ## ```{code-block-bg: true} Residual standard error: 6.651 on 13 degrees of freedom Multiple R-squared: 0.9432, Adjusted R-squared: 0.9388 F-statistic: 215.9 on 1 and 13 DF, p-value: 1.782e-09 ``` ::: incremental - Erro padrão dos resíduos e graus de liberdade - $R^{2}$ ($r$ de *Pearson* ao quadrado): indica o quanto de variabilidade na variável resposta é explicada pelas variáveis incluídas no modelo - neste caso, $94\%$ da altura pode ser explicada/prevista pela idade - $R^{2}$ ajustado é um ajuste a depender do número de variáveis preditoras incluídas no modelo (em regressão múltipla) - Teste-F é utilizado para comparação de modelos (se acrescentar variáveis preditoras melhoram o modelo) ::: ## Prevendo [mais]{.fg style="--col: #e64173"} dados não observados - $y = 62.5 + 7.5 \times x$ ::: incremental - Qual é a altura prevista pelo modelo para um recém-nascido? - $y = 62.5 + 7.5 \times 0$ - $y = 62.5$ ([63 centímetros!!!]{.fg style="--col: #e64173"}) - Qual é a altura prevista pelo modelo para alguém de 60 anos de idade? - $y = 62.5 + 7.5 \times 60$ - $y = 512.5$ ([5,13 metros!!!]{.fg style="--col: #e64173"}) - Por quê? ::: ## ::: incremental - Os coeficientes **não** são valores presentes nos dados, e **não** são valores do mundo real, são valores do **modelo** - *"All models are wrong, but some are useful"* (George E. P. Box) - *"The Golem of Prague"* (Richard McElreath) - Os dados (tipo, quantidade, variedade, representatividade, etc.) que alimentam/ajustam o modelo (*fit the model*) farão dele um modelo de estimativa melhor ou pior - Mas lembre-se: o modelo é apenas um robô e vai te obedecer! - Se você pedir uma reta, ela vai te dar a melhor reta ::: ## O quarteto de Anscombe (1973) ::: columns ::: {.column width="30%"} $\bar{X}$ de x = 9 $s$ de x = 3,3 $\bar{X}$ de y = 7,5 $s$ de y = 2 Corr de x e y = 0,816 Regressão linear: $y = 3+0,5x$ $R^2=0,67$ ::: ::: {.column width="70%"} 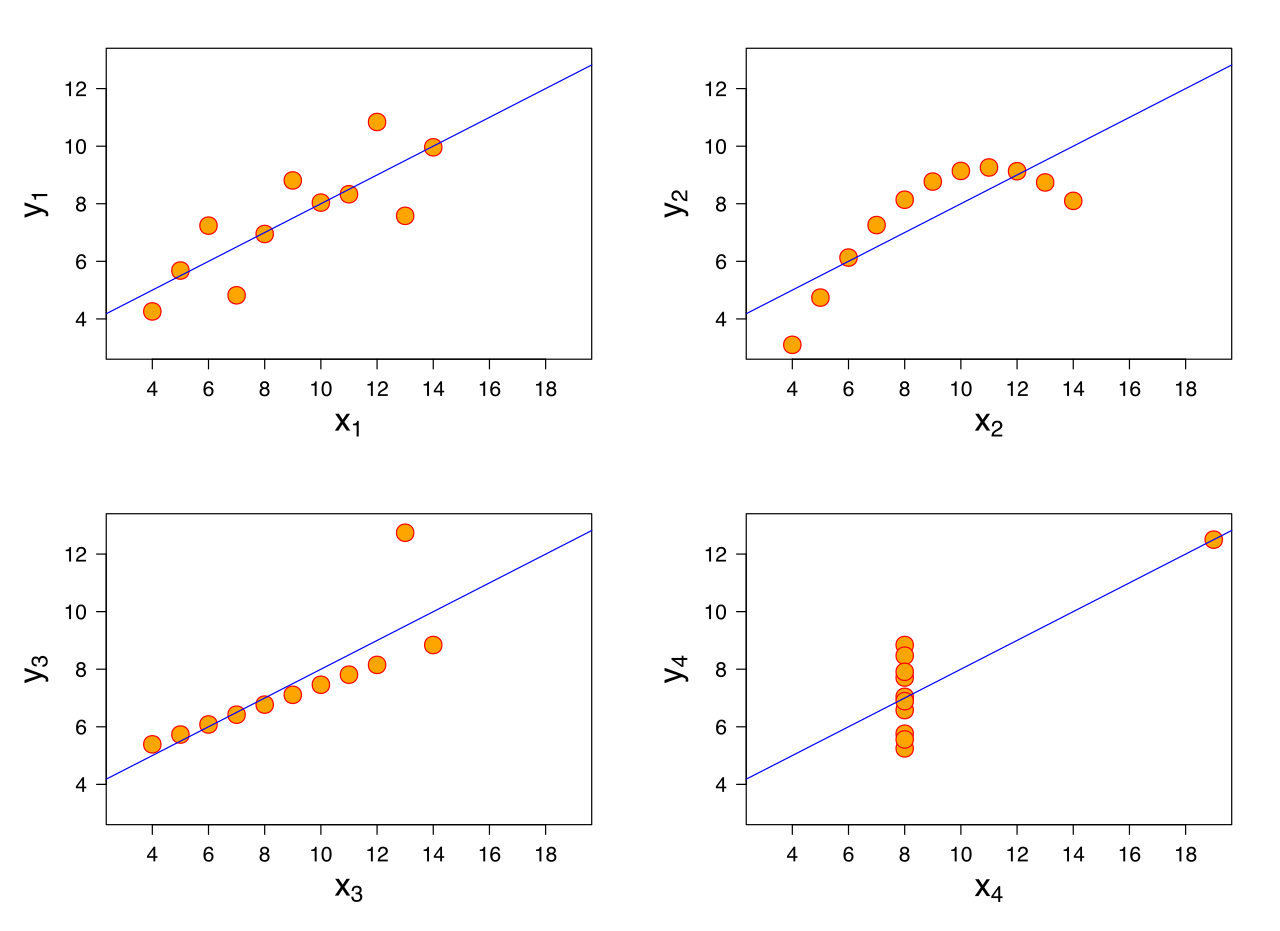{fig-align="center"} ::: ::: ## E se acrescentarmos dados de adultos ao nosso modelo de altura? ```r idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12, 17, 18, 19 ,22, 25, 26, 26, 28, 31, 32, 32, 35, 38, 40, 41, 45, 50, 55, 61, 62, 62, 63) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153, 170, 175, 168, 165, 180, 176, 171, 169, 181, 185, 175, 160, 170, 168, 170, 182, 177, 170, 172, 165, 166, 160) ex2 = data.frame(idade, altura) # Modelo modAltura2 = lm(altura ~ idade, data = ex2) modAltura2 # Visualizar linha de regressão ggplot(data = ex2, aes(x = idade, y = altura)) + geom_point() + geom_smooth(method = lm, se = F) ``` ## :::: {.columns} ::: {.column width="65%"} ```{r} library(tidyverse) # Criar dois vetores numéricos e colocá-los num dataframe idade = c(1, 2, 3, 4, 5, 5, 5, 6, 7, 8, 8, 9, 11, 12, 12, 17, 18, 19 ,22, 25, 26, 26, 28, 31, 32, 32, 35, 38, 40, 41, 45, 50, 55, 61, 62, 62, 63) altura = c(60, 65, 97, 98, 100, 105, 107, 105, 119, 122, 125, 132, 142, 147, 153, 170, 175, 168, 165, 180, 176, 171, 169, 181, 185, 175, 160, 170, 168, 170, 182, 177, 170, 172, 165, 166, 160) ex2 = data.frame(idade, altura) # Modelo modAltura2 = lm(altura ~ idade, data = ex2) modAltura2 # Visualizar linha de regressão ggplot(data = ex2, aes(x = idade, y = altura)) + geom_point() + geom_smooth(method = lm, se = F) + theme_minimal() ``` ::: ::: {.column width="35%"} - Se você pedir uma reta, o modelo vai gerar uma reta! - Nosso modelo certamente não serve para dados de adultos - [O que fazer?]{.fg style="--col: #e64173"} ::: ::: # Exemplo Linguístico 1 {background-color="#40666e"} ## Modelo com previsor numérico{auto-animate="true"} - Dados `english` do pacote `languageR` - Dados de tempo de reação (em log) de decisão lexical de 2284 substantivos e verbos do inglês com 34 variáveis preditoras sociais e linguísticas - Estimar o tempo de reação em função da familiaridade com a palavra ```r # Carregar os dados "english" do pacote LanguageR library(languageR) data(english) ``` ## Modelo com previsor numérico{auto-animate="true"} - Dados `english` do pacote `languageR` - Dados de tempo de reação de decisão lexical de 2284 substantivos e verbos do inglês com 34 variáveis preditoras sociais e linguísticas - Estimar o tempo de reação em função da familiaridade com a palavra ```r # Carregar os dados "english" do pacote LanguageR library(languageR) data(english) # Plotar Tempo de Reação por Familiaridade (com a palavra) ggplot(data = english, aes(x = Familiarity, y = RTlexdec)) + geom_point() + theme_classic() ``` ## ```{r} # Carregar os dados "english" do pacote LanguageR library(languageR) data(english) # Plotar Tempo de Reação por Familiaridade (com a palavra) ggplot(data = english, aes(x = Familiarity, y = RTlexdec)) + geom_point() + theme_classic() ``` . . . - Conseguem ver alguma associação/correlação? ## ```{r} #| echo: true #| output-location: fragment ggplot(data = english, aes(x = Familiarity, y = RTlexdec)) + geom_point(alpha = 0.3) + geom_smooth(method = lm) + labs(x = "Familiaridade com a palavra", y = "Tempo de reação") + theme_classic() ``` ## Estimar tempo de reação em função da familiaridade com a palavra ```{r} #| echo: true #| output-location: fragment modEn = lm(RTlexdec ~ Familiarity, data = english) summary(modEn) ``` ## Estimar tempo de reação em função da familiaridade com a palavra ::: columns ::: {.column width="70%"} ```{r} #| echo: true modEn = lm(RTlexdec ~ Familiarity, data = english) summary(modEn) ``` ::: ::: {.column width="30%"} ::: incremental - O que quer dizer o intercepto ($\beta_0$) de $6.78$? - O que quer dizer o slope ($\beta_1$) de $-0.06$? - Qual é o poder explicativo deste modelo? ::: ::: ::: # Exemplo Linguístico 2 {background-color="#40666e"} ## Modelo com previsor categórico ::: incremental - Dados `english` do pacote `languageR` - Estimar o tempo de reação em função da faixa etária dos participantes (codificada nos dados em `old` e `young`) - Qual seria a hipótese lógica? ::: . . . ```r # Plotar Tempo de Reação por faixa etária ggplot(data = english, aes(x = AgeSubject, y = RTlexdec)) + geom_boxplot() + theme_classic() ``` ## ```{r} ggplot(data = english, aes(x = AgeSubject, y = RTlexdec)) + geom_boxplot() + theme_classic() ``` ## Estimar tempo de reação em função da faixa etária ```{r} #| echo: true #| output-location: fragment modEn2 = lm(RTlexdec ~ AgeSubject, data = english) summary(modEn2) ``` ## Estimar tempo de reação em função da faixa etária ::: columns ::: {.column width="70%"} ```{r} #| echo: true modEn2 = lm(RTlexdec ~ AgeSubject, data = english) summary(modEn2) ``` ::: ::: {.column width="30%"} ::: incremental - O que quer dizer o intercepto ($\beta_0$) de $6.66$? - O que quer dizer o slope ($\beta_1$) de $-0.22$? - Qual é o poder explicativo deste modelo? ::: ::: ::: # Momento mão na massa! {background-color="#40666e"} ## Slides / códigos: {fig-align="center"} ## Tarefa 1: - Usando os dados `english` do pacote `languageR`: - estime o **tempo de reação** (`RTlexdec`) em função da **frequência escrita da palavra** (`WrittenFrequency`) - Gere um gráfico que mostre a relação entre essas variáveis - Antes de ajustar o modelo: - qual seria a hipótese lógica? - Após ajustar o modelo: - Qual é o valor de $\beta_0$? O que ele representa? - Qual é o valor de $\beta_1$? O que ele representa? - O modelo prevê um efeito de frequência escrita da palavra sobre o tempo de reação? - Qual é o poder explicativo do modelo? ## Tarefa 2: - Usando os dados `english` do pacote `languageR`: - estime o **tempo de reação** (`RTlexdec`) em função da **categoria da palavra** (`WordCategory`), se verbo ou substantivo (codificados em `V` e `N`) - Gere um gráfico que mostre a relação entre essas variáveis - Antes de ajustar o modelo: - há uma hipótese lógica? - Após ajustar o modelo: - Qual é o valor de $\beta_0$? O que ele representa? - Qual é o valor de $\beta_1$? O que ele representa? - O modelo prevê um efeito de ser substantivo ou verbo sobre o tempo de reação? - Qual é o poder explicativo do modelo? # Regressão Linear Múltipla {background-color="#40666e"} ## Nos dados `english` vimos o efeito de **familiaridade** com a palavra e o de **faixa etária** sobre o **tempo de reação** em modelos separados: . . . ::: {.columns} ::: {.column width="50%"} ```{r} #| echo: true modEn = lm(RTlexdec ~ Familiarity, data = english) modEn summary(modEn)$r.squared ``` ::: ::: {.column width="50%"} ```{r} #| echo: true modEn2 = lm(RTlexdec ~ AgeSubject, data = english) modEn2 summary(modEn2)$r.squared ``` ::: ::: ## E se juntarmos as duas variáveis preditoras no mesmo modelo? ::: incremental - Regressão Linear **Múltipla** - se na simples tínhamos $y = \beta_0+\beta_1x$ - na múltipla temos $y = \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3...$ - no nosso caso: $tempoReção = \beta_0+\beta_1\times idade +\beta_2\times familiaridade$ - forneceremos vários valores de **tempo de reação**, **idade** e **familiaridade**, e queremos que o modelo estime $\beta_0$ e $\beta_1$ ::: . . . > "*we live in a multifactorial world in which probably no phenomenon is really monofactorial -- probably just about everything is correlated with several things at the same time*". (Gries, Stefan Th 2013) ## Como visualizar as associações das três variáveis em um mesmo gráfico? . . . ```{r} #| echo: true #| output-location: fragment ggplot(english, aes(x=Familiarity, y=RTlexdec, color=AgeSubject)) + geom_point(alpha=.3) + geom_smooth(method = lm) + theme_light() ``` ## Modelo ```{r} #| echo: true #| output-location: fragment modEn3 = lm(data = english, RTlexdec ~ Familiarity + AgeSubject) summary(modEn3) ``` ## Modelo ::: {.columns} ::: {.column width="70%"} ```{r} summary(modEn3) ``` ::: ::: {.column width="30%"} - Como interpretar: - $\beta_0$? - $\beta_1$? - $\beta_2$? - $\hat{R}$? ::: ::: ::: incremental - Qual é o tempo de reação estimado pelo modelo de um **velho** a uma palavra de **familiaridade 1**? - E de um **jovem** a uma palavra de **familiaridade 4**? ::: ## Comparação dos modelos - É melhor ajustar e reportar os [2 modelos simples]{.fg style="--col: #e64173"} separadamente ou o [modelo múltiplo]{.fg style="--col: #e64173"}? . . . ::: {.columns} ::: {.column width="33%"} ```{r} #| echo: true summary(modEn)$r.squared summary(modEn)$fstatistic[1] ``` ::: ::: {.column width="33%"} ```{r} #| echo: true summary(modEn2)$r.squared summary(modEn2)$fstatistic[1] ``` ::: ::: {.column width="33%"} ```{r} #| echo: true summary(modEn3)$r.squared summary(modEn3)$fstatistic[1] ``` ::: ::: . . . - Um valor de F maior indica que incluir as variáveis melhorou o poder explicativo do modelo - Podemos rodar `anova(modelo1, modelo2)` para comparar estatisticamente os valores de F (`p<0.05` indica que o modelo mais complexo é superior) ## Podemos incluir quantas variáveis preditoras em um modelo de regressão? ::: incremental - Tantas quanto ...? Tivermos? Quisermos? Forem necessárias/motivadas/coerentes/lógicas? - Atenção: - Navalha de Occam - Multicolinearidade - Interação - Pensar/Modelar possíveis relações de causalidade antes (remover variáveis de confusão) $\rightarrow$ DAGs ::: # Mais mão na massa! {background-color="#40666e"} ## Slides / códigos: {fig-align="center"} ## Tarefa 3: - Usando os dados `english` do pacote `languageR`: - estime o **tempo de reação** (`RTlexdec`) em função da **familiaridade** com a palavra (`Familiarity`) + **faixa etária** (`AgeSubject`) + **frequência escrita da palavra** (`WrittenFrequency`) - interprete os coeficientes e verifique o poder explicativo do modelo - [Desafio]{.fg style="--col: #e64173"}: Como gerar um gráfico que mostre a relação das 4 variáveis? ## Tarefa 4: - Acrescente ao modelo anterior a variável **categoria da palavra** (`WordCategory`) - interprete os coeficientes e verifique o poder explicativo do modelo - Compare a significância de `WordCategory` quando estava em um modelo simples com sua significância neste modelo - Compare o poder explicativo deste modelo ao do anterior - [Bônus]{.fg style="--col: #e64173"}: podemos usar `anova(modelo1, modelo2)` para comparar modelos (`p<0.05` indica que o modelo mais complexo é superior)